北航——空气动力学（上）

第一讲：空气动力学基础绪论

1.概论

1.1空气动力学的概念

物质的三态：

物质的三态划分	特点	静止状态下的受力情况
固体	具有固定的形状和体积。	可以承受拉力、压力和剪切力。
液体	具有固定的体积，无固定的形状。	只能承受压力，几乎不能承受拉力和剪切力。
气体	无固定的体积，也无固定的形状。	只能承受压力，几乎不能承受拉力和剪切力。

【流体】：是液体和气体的统称，特点是易流动性，在静止状态下不能承受剪力。

【空气动力学】：流体力学的一个分支，研究流体（空气）处于平衡和机械运动规律及其应用的学科。

1.2空气动力学的研究对象

相对飞行原理（空气动力学实验原理）：

当飞行器以某一速度在静止空气中运动时，飞行器与空气的相对运动规律和相互作用力，
与飞行器固定不动而让空气以同样大小和相反方向的速度流过飞行器的情况是等效的。

1.3空气动力学的分类

按照研究对象的运动速度：

低速空气动力学：
高速空气动力学：亚声速空气动力学，跨声速空气动力学，超声速空气动力学

按照研究对象：

飞行器空气动力学

飞行器在大气中飞行时的空气动力学问题
工业空气动力学

鼓风机、涡轮机、风力发电机的气动力问题
房屋、坑道通风，高层建筑的风压
汽车、高速列车的阻力

1.4空气动力学的研究方法

空气动力学的研究方法：

实验研究—实验空气动力学
理论研究—理论空气动力学
数值计算—计算空气动力学

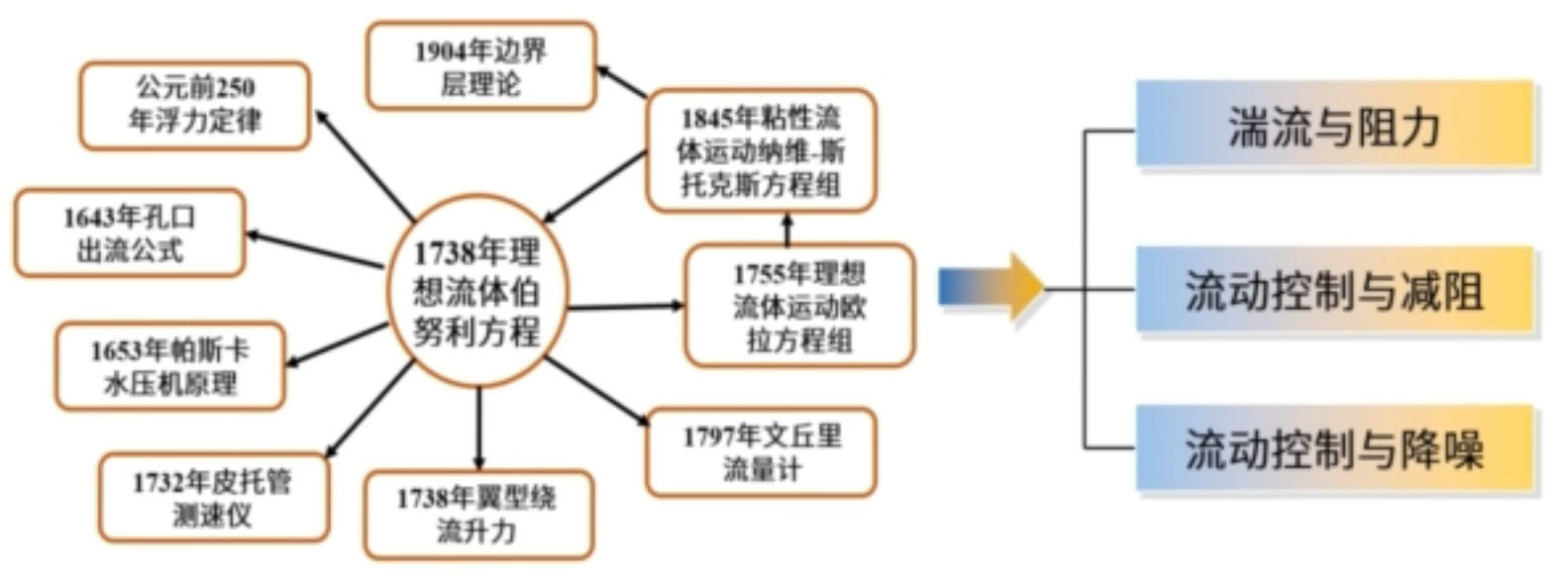
1.5空气动力学的发展过程

定性实验和定性认识阶段：理想流体理想气体的扰流的空气动力学问题，解决升力问题。

粘性流体力学的研究时代：解决飞行阻力问题，包括湍流以及对流动的控制和减阻。

微积分的出现和连续介质力学的应用是空气动力学发展的基础。

空气动力学的研究

第二讲：流体（空气）的力学属性

1.连续性假设

流体是由连续无间隙地充满所占据空间的流体质点组成。
流体质点所具有的宏观物理量满足一切物理定律。

每一个流体质点在任一时刻只能占据一个空间点，而不能占据两个以上空间点，
确保流体质点的物理量在空间上不出现间断；

每一个空间点在任一时刻只能被一个流体质点所占据，而不能被两个以上质点所占据，
确保流体质点物理量在空间上不出现多值。

【努生数 $K_n$ 】：分子平均自由程与物体特征尺寸之比 $K_n=l/L$ ，是判断流体是否满足连续介质假设的依据。

努生数 $K_n$	判定	补充
$K_n\leq 0.01$	连续流	可采用连续性假设，利用物体运动的普遍定律研究流体连续运动的规律。
$0.01<K_n\leq 1$	滑移流
$1<K_n\leq 10$	过渡流
$K_n>10$	分子流（离散流）	采用离散流假设，直接用分子运动的波尔兹曼方程来描述流体运动。

在连续性介质的前提下，流体介质的密度表示为： $\rho=\frac{\Delta m}{\Delta \tau }$ ，
在空间中取$\tau $体积，并比上该体积中所具有的质量。

当切换到非均匀介质的前提，该空间中的介质分布是随机的
此时，流体介质的密度应当表示为 $\Delta \tau \rightarrow 0,\rho=lim\frac{\Delta m}{\Delta \tau }$

2.流体的特性

2.1流体的易流性

在宏观上，流体与固体在力学上最本质的区别是二者所承受的剪应力和剪切变形的关系。

固体的剪应力与剪切变形量$\theta $成正比。流体的角变形量除了与剪应力$ \tau $有关外，还与剪切应力$ \tau $的持续时间有关。

剪应力与剪切变形量的关系

【易流性】：不论所加剪切应力τ多么小，只要不等于零，流体都将在剪应力作用下持续不断的产生变形运动(流动)。

2.2流体的压缩性与弹性

【压缩性】：流体在受压时，体积发生改变的属性。

【弹性】：流体抵抗压缩变形的能力称为弹性。

【体积弹性模量】：压缩单位体积相对量所需的压强值，用来度量流体的弹性。大的 $E$ 值不易被压缩，反之小值容易被压缩。

$E=\frac{dp}{dV/V }（N/m^2,Pa）\\引入dm=d（\rho V）=0\\E=\frac{dp}{dV/V }=\rho \frac{dp}{d\rho }$

在空气动力学中，是否要考虑压缩性，主要看空气流动速度的大小。

2.3流体的粘性

【牛顿内摩擦定律】：拖曳移动平板的剪切力 $F$ ，正比于上板的移动速度 $U$ 和板的面积 $A$ ，而反比于平板之间的间距 $h$ 。

$$ F\propto \frac{U}{h}A，\tau =\mu \frac{U}{h} $$ 式中：$μ$——比例系数，反映了粘性大小的物性参数，称为动力粘性系数。

【粘性】：流体相邻层间存在着抵抗层间相互运动的趋势。单位， $Ns/m^2,Pa\cdot s$
$\mu _{空气}=1.7894\times 10^{-5}kg/m/s；\mu _{水}=1.139\times 10^{-3}kg/m/s$

牛顿内摩擦定律可以看出：

流体的剪应力与压强无关（注意到固体摩擦力与正压力有关)。
无论剪应力多小，流体都会发生变形运动。只要剪应力存在，速度梯度就不为0。
只要流体静止或无变形，就不存在剪应力，换言之，流体不存在静摩擦力。
由于流体与固体表面无滑移，故壁面处的速度梯度为有限值所以壁面处剪应力也为有限值。

流体的粘性：

液体：温度升高，动力粘性系数变小，反之变大。

气体：温度升高，动力粘性系数变大，反之变小。

气体动力粘性系数的萨特兰公式：

用于计算空气动力粘滞系数的近似公式：

$\frac{\mu }{\mu_0}=(\frac{T}{T_0})^{1.5}\frac{T_0+110.4}{T+110.4}\\T_0=288.15k,\mu_0=1.7894\times 10^{-5}Pa\cdot s$

【运动粘性系数】：单位质量的粘性系数为运动粘性系数。 $\nu =\frac{\mu }{\rho}$
$\nu _{空气}=1.139\times 10^{-6}m^2/s；\nu _{水}=1.461\times 10^{-5}m^2/s$

对于小粘性系数流体，在某些流动中可忽略粘性作用。把不考虑粘性的流体称为理想流体。

binghan流体，泥浆、血浆、牙膏等，存在一个初始的变形切应力；
伪塑性流体，尼龙、橡胶、油漆、绝缘，粘性系数与速度梯度的变形率的开方成反比，变形率越大速度粘性系数越小；
牛顿流体，水、空气、汽油、酒精等；
胀塑性流体，生面团、浓淀粉糊等，粘性系数随变形率的增大而增大。
理想流体，无粘流体。

(1) $\tau=\tau_0+\mu \frac{d u}{d y}$
(2) $\tau=\mu\left(\frac{d u}{d y}\right)^{0.5}=\frac{\mu}{\sqrt{\frac{d u}{d y}}} \frac{d u}{d y}=\eta \frac{d u}{d y}, \eta=\frac{\mu}{\sqrt{\frac{d u}{d y}}}$
(3) $\tau=\mu \frac{d u}{d y}$
(4) $\tau=\mu\left(\frac{d u}{d y}\right)^2=\mu \frac{d u}{d y} \frac{d u}{d y}=\eta \frac{d u}{d y}, \eta=\mu \frac{d u}{d y}$
(5) $\tau=0 \frac{d u}{d y}=0$

3.作用在流体微团上的力的分类

按物理意义划分：惯性力、重力、弹性力、摩擦力等。

按作用方式划分：表面力和质量力（彻体力，体积力）。

单位质量的质量力： $f/m=a$

可以将流体微团表面所受到的力分为法向力与切向力，
指向作用面内的法向应力称为压强， $P=\lim_{\Delta A\rightarrow 0}\frac{\Delta P}{\Delta A}$ ， $N/m^2(Pa)$
切向力与作用面相切， $\tau=\lim_{\Delta A\rightarrow 0}\frac{\Delta T}{\Delta A}$ ，由流体的粘性产生，只在流动时才存在。

上述画出的表面力对整个流体而言是内力，对所画出的流体微团来说则是外力。

在静止流体或者无粘流体中，其内部粘性系数为0，受力也只有内法向应力，即压强。

第三节：流体（空气）静力学

1.压强特性

静止流体内任一点的压强及其各向同性特征

方向垂直指向作用面；
大小与作用面的方位无关，任意一点的压强仅是坐标位置的单值连续函数。

$$ p=p（x,y,z）\\p_x\frac{1}{2}dydz-p_ndscos(n,x)=0\\dscos(n,x)=\frac{1}{2}dydz $$ 故，证明： $$ p_x=p_n\\p_y=p_n\\p_z=p_n $$ 因为，$n$的方向是任意的，故各向同性得证。(这点与固体内任意一点的应力状态是不同的)

2.流体静力平衡微分方程

假设：

六面体体积: $d \tau=d x d y d z$
中心点压强：p=p $(x, y, z)$
中心点密度： $\rho=\rho \quad(x, y, z)$
单位质量力: $f_x, f_y, f_z$

x方向的表面力为: $\left(p-\frac{\partial p}{\partial x} \frac{d x}{2}\right) d y d z-\left(p+\frac{\partial p}{\partial x} \frac{d x}{2}\right) d y d z=-\frac{\partial p}{\partial x} d x d y d z$

$\mathrm{x}$ 方向的质量力为: $f_x \rho d x d y d z$

流体静止, 则x方向的合外力为零: $-\frac{\partial p_p}{\partial x} d x d y d z+f_x \rho d x d y d z=0$

平衡方程组的导出：

两边同除以 $d \tau=d x d y d z$ 并令 $d \tau$ 趋于零, 可得 $x$ 方向平衡方程:

$f_x-\frac{1}{\rho} \frac{\partial p}{\partial x}=\mathbf{0}$

两边同除以 $d \tau=d x d y d z$ 并令 $d \tau$ 趋于零, 可得方向 $x$ 平衡方程:

$f_x-\frac{1}{\rho} \frac{\partial p}{\partial x}=0$

将上三个式子分别乘以 $\mathrm{dx}, \mathrm{dy}, \mathrm{dz}$ , 然后相加起来, 得到：

$\frac{\partial p}{\partial x} d x+\frac{\partial p}{\partial y} d y+\frac{\partial p}{\partial z} d z=\rho\left(f_x d x+f_y d y+f_z d z\right)$

此式左端是压强的全微分

$d p=\frac{\partial p}{\partial x} d x+\frac{\partial p}{\partial y} d y+\frac{\partial p}{\partial z} d z$

如果沿着任意封闭曲线积分，得到

$\oint_C \frac{d p}{\rho(p)}=\oint_C\left(f_x d x+f_y d y+f_z d z\right)=\mathbf{0}$

流体处于静止状态下，单位质量力积分与路径无关。也就是说，单位质量力是有势力。
由此得到，在静止状态下，所受的质量力必须是有有势力

等压面的定义：

流场中压强相等的空间点组成的几何曲面或平面。

在等压面上满足： $dp=0$ 或者， $f_xdx+f_ydy+f_zdz=0$ ；
（f表示质量力），若质量力与线段的微量均不等于0，但是乘积为0，则满足 $\vec{f_v}\cdot \vec{d_r}=0$ ，表示质量力与等压面正交。

3.重力场静止液体中的压强分布规律

重力作用下，平衡液体的基本方程。

$\frac{p}{\gamma }+z=H(常数)$

上式表明，在重力作用下，平衡液体中 $\frac{p}{\gamma }$ 与 $z$ 之和为常数。显然，静止液体中等压面为水平面 $z=c$ 。

式中：

$z$ ——代表所研究液体质点在坐标系中所处高度，称为位置水头
$\frac{p}{\gamma }$ ——代表所研究液体质点在真空管中上升高度，称为压力水头
$H$ ——由于方程量纲为高度，该积分常数代表上述二高度之和称为总水头，或测压管水头。

表示从封闭容器中任意点打孔，联通外界的真空管中液体高度是一致的。

静止液体中，压力水头与位置水头可以互相转换但总水头保持不变。

假设自由液面距水平轴距离为 $H'$ ,则自由面与 $z$ 处流体满足：

$\frac{p}{\gamma }+z=\frac{p_0}{\gamma }+H'$

即， $p=p_0+\gamma (H'-z)$ ； $(H'-z)$ 表示自由面以下的深度，亦可以用 $h$ 代替。

得到结论：

==平衡流体中距自由面深h处的压强的贡献：==
1.上方单位面积上的液柱重量 $\gamma h$ ,因此压强随距自由面的淹没深度而线性增加。
2.自由面上的压强贡献 $p_0$ ，而该贡献处处相同与深度无关

==当自由面为大气压 $p_a$ 时，距自由面深处的压强可表为：== $p=p_a+\gamma h$

故，静止流体若在其内某一点位置有一个压强增量，这个增量也会等量得传递到液体内部的任一点上。

压强的计量：

【绝对压强】：以绝对真空为压强参考值计量的压强

【相对压强】：以大气压 $p_a$ 为参考压强计量的压强

【真空度】：以大气压 $p_a$ 为参考压强，不足大气压部分的压强， $p_v=p_a-p$

第四讲：描述流体（空气）运动的方法

描述流体（空气）运动的方法：拉格朗日方法（质点系法）和欧拉方法(空间点法，流场法)

1.拉格朗日方法（质点系法）

观察者跟随每个流体质点，观察质点的运动行为，从而记录质点的运动历程，分析运动规律。

流体质点的标识：

每个流体质点在t时刻的位置为 $x(a,b,c,t),y(a,b,c,t),z(a,b,c,t)$ ，
跟着特定的流体质点 $（a,b,c）$ 在不同 $t$ 时刻下的空间位置 $（x.y.z）$

$a,b,c$ 为流体质点的标识符， $t$ 表示时间。 $a,b,c，t$ 被称为拉格朗日变数。

对于给定流体质点，速度表达式是：

$u=\frac{\partial x(a,b,c,t)}{\partial t} ,v=\frac{\partial y(a,b,c,t)}{\partial t} ,w=\frac{\partial z(a,b,c,t)}{\partial t}$

流体质点的加速度为：

$a_x=\frac{\partial^2 x(a,b,c,t)}{\partial t^2} ,a_y=\frac{\partial^2 y(a,b,c,t)}{\partial t^2} ,a_z=\frac{\partial^2 z(a,b,c,t)}{\partial t^2}$

迹线方程：同一流体质点在不同时刻下走过的轨迹

$\frac{dx}{u}=\frac{dy}{v}=\frac{dz}{w}=dt$

2.欧拉方法(空间点法，流场法)

观察者相对于坐标系固定不动，着眼于不同流体质点通过空间固定点的流动行为。

速度表示：

给定一个固定空间点 $x,y,z$ ，给出在 $t$ 时刻下的占据该位置的流体质点的速度。

$\left\{\begin{array}{l} u(x, y, z, t) \\ v(x, y, z, t) \\ w(x, y, z, t) \end{array}\right. \\\vec{V}=u\vec{i}+v\vec{j}+w\vec{k}$

将 $x,y,z,t$ 称之为欧拉变数。

$x,y,z$ 给定、 $t$ 变化，表示不同时刻不同流体质点通过同一空间点的速度。
$t$ 给定、 $x,y,z$ 变化，表示给定时刻，不同流体质点通过不同空间点的速度，描述速度场。

【流场】：一个布满了某种物理量的空间称为场。流体流动所占据的空间称为流场。

加速度的表达：

引起流体质点速度的变化来自于两方面的贡献：其一是流场的不均匀性；其二是流场的非定常性。

不均匀性表示空间位置的变化引起的速度变化，非定常性表示由于液体压强改变所造成的速度变化。

推导：

设某一流体质点在 $t$ 时刻位于流场中 $M$ 点，经过微分时段位于 $N$ 点，根据加速度定义有

$\vec{a}=\frac{d \vec{V}}{d t}=\lim _{\Delta \rightarrow 0} \frac{\Delta \vec{V}}{\Delta t}=\lim _{\Delta t \rightarrow 0} \frac{\vec{V}(N, t+\Delta t)-\vec{V}(M, t)}{\Delta t}\\ \frac{d \vec{V}}{d t}=\lim _{\Delta \rightarrow 0} \frac{\vec{V}(N, t+\Delta t)-\vec{V}(N, t)}{\Delta t} \quad+\lim _{\Delta \rightarrow 0} \frac{\vec{V}(N, t)-\vec{V}(M, t)}{\Delta t} \\$

前一部分 $\lim _{\Delta \rightarrow 0} \frac{\vec{V}(N, t+\Delta t)-\vec{V}(N, t)}{\Delta t}$ ，表示同一个空间点在不同时刻下的速度的增量，由流场的非定常性引起；
后一部分 $\lim _{\Delta \rightarrow 0} \frac{\vec{V}(N, t)-\vec{V}(M, t)}{\Delta t}$ ，表示同一时刻下由于空间位置变化引起的加速度，是流场不均匀性的表现。

根据泰勒展开，流场非定常性引起的速度变化：

$\vec{V}(N, t+\Delta t)=\vec{V}(N, t)+\frac{\partial \vec{V}(N, t)}{\partial t} \Delta t+O\left(\Delta t^2\right)\\\lim _{\Delta \rightarrow 0} \frac{\vec{V}(N, t+\Delta t)-\vec{V}(N, t)}{\Delta t}=\lim _{\Delta \rightarrow 0} \frac{\frac{\partial \vec{V}(N, t)}{\partial t} \Delta t+O\left(\Delta t^2\right)}{\Delta t}=\frac{\partial \vec{V}(M, t)}{\partial t}=\frac{\partial \vec{V}}{\partial t}$

由于流场不均匀性引起的速度变化：

$\begin{aligned} & \\ & \vec{V}(N, t)=\vec{V}(x+\Delta x, y+\Delta y, z+\Delta z, t) \\ & =\vec{V}(x, y, z, t)+\frac{\partial \vec{V}(x, y, z, t)}{\partial x} \Delta x+\frac{\partial \vec{V}(x, y, z, t)}{\partial y} \Delta y+\frac{\partial \vec{V}(x, y, z, t)}{\partial z} \Delta z+O\left(\Delta x^2, \ldots,\right) \\ \end{aligned}$

**重要说明：**由于跟随性， $\Delta x/\Delta t=u$

$\begin{aligned} & \lim _{\Delta \rightarrow 0} \frac{\vec{V}(N, t)-\vec{V}(M, t)}{\Delta t} \\ & =\lim _{\Delta \rightarrow 0} \frac{\frac{\partial \vec{V}(M, t)}{\partial x} \Delta x+\frac{\partial \vec{V}(M, t)}{\partial y} \Delta y+\frac{\partial \vec{V}(M, t)}{\partial z} \Delta z+O\left(\Delta x^2, \ldots .\right)}{\Delta t} \\ & =\lim _{\Delta \rightarrow 0} \frac{\Delta x}{\Delta t} \frac{\partial \vec{V}(M, t)}{\partial x}+\lim _{\Delta \rightarrow 0} \frac{\Delta y}{\Delta t} \frac{\partial \vec{V}(M, t)}{\partial y}+\lim _{\Delta \rightarrow 0} \frac{\Delta z}{\Delta t} \frac{\partial \vec{V}(M, t)}{\partial z} \\ & =u \frac{\partial \vec{V}(M, t)}{\partial x}+v \frac{\partial \vec{V}(M, t)}{\partial y}+w \frac{\partial \vec{V}(M, t)}{\partial z} \\ \end{aligned}$

综合，得到流体质点的全加速度为：

$\begin{aligned} &\vec{a}=\frac{d \vec{V}}{d t}=\frac{\partial \vec{V}}{\partial t}+u \frac{\partial \vec{V}}{\partial x}+\mathrm{v} \frac{\partial \vec{V}}{\partial y}+w \frac{\partial \vec{V}}{\partial z} \\ &\vec{a}=\frac{d \vec{V}}{d t}=\frac{\partial \vec{V}}{\partial t}+(\vec{V} \cdot \nabla) \vec{V} \\ \end{aligned}$

全加速度， $\frac{\partial \vec{V}}{\partial t}$ 由流场非定常性引起；迁移加速度（对流加速度）， $u \frac{\partial \vec{V}}{\partial x}+\mathrm{v} \frac{\partial \vec{V}}{\partial y}+w \frac{\partial \vec{V}}{\partial z}$ ，由于流场的不均匀性引起。

跟随条件是：$ d x=u d t, d y=v d t, d z=w d t$

全加速度（随体加速度）的表示：

$\begin{aligned} & \frac{d u}{d t}=\frac{\partial u}{\partial t}+u \frac{\partial u}{\partial x}+v \frac{\partial u}{\partial y}+w \frac{\partial u}{\partial z} \\ & \frac{d v}{d t}=\frac{\partial v}{\partial t}+u \frac{\partial v}{\partial x}+v \frac{\partial v}{\partial y}+w \frac{\partial v}{\partial z} \\ & \frac{d w}{d t}=\frac{\partial w}{\partial t}+u \frac{\partial w}{\partial x}+v \frac{\partial w}{\partial y}+w \frac{\partial w}{\partial z} \\ \end{aligned}$

随体导数算子：

$\begin{aligned} & \frac{d}{d t}=\frac{\partial}{\partial t}+u \frac{\partial}{\partial x}+v \frac{\partial}{\partial y}+w \frac{\partial}{\partial z} \end{aligned}$

该随体算子对于流场中其他物理量也适用，例如压强 $P$ 或者温度 $T$

$\begin{aligned} & \frac{d p}{d t}=\frac{\partial p}{\partial t}+u \frac{\partial p}{\partial x}+v \frac{\partial p}{\partial y}+w \frac{\partial p}{\partial z} \\ & \frac{d T}{d t}=\frac{\partial T}{\partial t}+u \frac{\partial T}{\partial x}+v \frac{\partial T}{\partial y}+w \frac{\partial T}{\partial z} \\ \end{aligned}$

该式在传热领域的意义： $\frac{\partial T}{\partial t}$ ，表示热传递引起的热温度变化；$u \frac{\partial T}{\partial x}+v \frac{\partial T}{\partial y}+w \frac{\partial T}{\partial z} $，表示由于热对流引起的温度变化

将流动表示一维空间流程坐标 $s$ 和时间 $t$ 的函数，速度场为 $v(s,t)$

$a_s=\frac{D v}{D t}=\frac{\partial v}{\partial t}+v \frac{\partial v}{\partial s}$

$\frac{\partial v}{\partial t}$ ，由流场非定常性引起(压强变化，水面位置)；$ v \frac{\partial v}{\partial} $，由于流场的不均匀性引起（位置变化，管径）。

【流线】：在某一瞬时，在流场中存在一条曲线，任何一点的切线方向均与占据该点的流体质点速度方向一致，这样的曲线称为流线。
同一时刻下，不同流体质点所留下的轨迹曲线。

流线微分方程：

$\frac{dx}{u}=\frac{dy}{v}=\frac{dz}{w}=\frac{ds}{V}$

流线的性质：

在定常流动中，流体质点的迹线与流线重合。在非定常流动中，流线和迹线一般是不重合的。
在定常流动中，流线是流体不可跨越的曲线。
在常点处，流线不能相交、分叉、汇交、转折，流线只能是一条光滑的曲线。
也就是，在同一时刻，一点处只能通过一条流线。
在奇点和零速度点例外。

第五讲：流体（空气）微团的运动形式

1.流体微团的基本运动形式

理论力学研究的刚体或者质点，被视为无变形的对象，其运动形式包括：平动和转动。

在流体力学中，研究对象是由质点组成的不断变化形状与大小的微团，其运动形式除包括了刚体的运动形式外，还有变形运动。

变形运动包括两种·：

引起体积大小变化的边长伸缩线变形运动
引起体积形状变化的角变形运动。

变形体的基本运动形式：

基本运动形式	内涵	图示
平动	微团内部每一点位置上的速度一致
转动	角平分线旋转，边长形状不变
线变形运动	线性长度的边长发生变化
角变形运动	当角平分线在流体微团运动的时候没有旋转

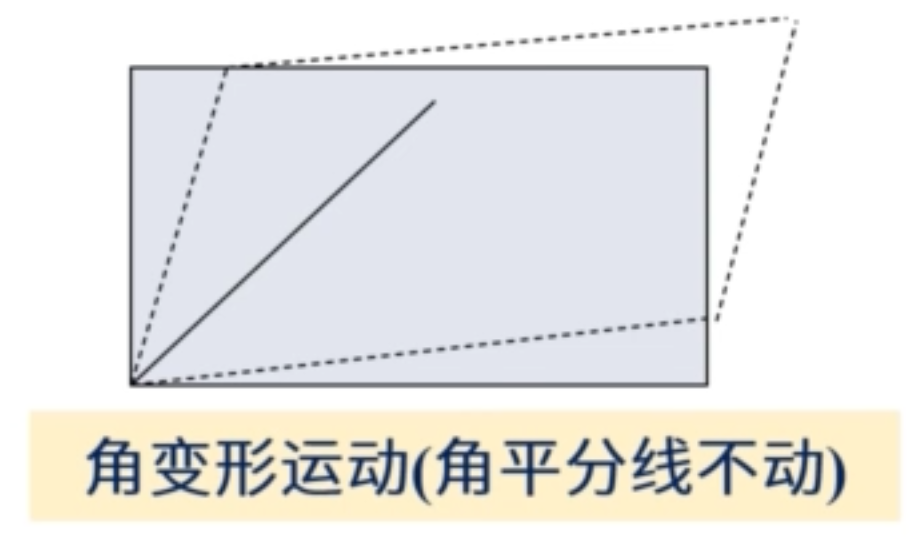2.流体微团的运动形式分解

2.1线变形运动与线变形率

线变形运动：微元体各边长发生伸缩的运动。
【线变形速率】：单位时间单位长度的线变形量。

如对于AB边长，在微分时段内边长的增加量为

$\Delta \left ( AB \right )=\left [ u+\frac{\partial u}{\partial x}-u \right ]\Delta t=\frac{\partial u}{\partial x}\Delta x\Delta t$

$x$ 方向的线变形速率为 $\theta_x=\lim _{\Delta x \rightarrow 0} \frac{\Delta(A B)}{\Delta t \Delta x}=\frac{\partial u}{\partial x}$

$y$ 方向的线变形速率为 $\theta_y=\lim _{\Delta \rightarrow 0} \frac{\Delta(A C)}{\Delta t \Delta y}=\frac{\partial v}{\partial y}$

平面微团的面积变化率为

$\begin{aligned} & d i \vec{V}=\lim _{\Delta \rightarrow 0} \frac{\Delta(A B \times A C)}{\Delta x \Delta y \Delta t}=\lim _{\Delta \rightarrow 00} \frac{\left(\Delta x+\frac{\partial u}{\partial x} \Delta x \Delta t\right)\left(\Delta y+\frac{\partial \mathrm{v}}{\partial y} \Delta y \Delta t\right)-\Delta x \Delta y}{\Delta x \Delta y \Delta t} \\ & =\lim _{\Delta \rightarrow \rightarrow 0} \frac{\left(\frac{\partial u}{\partial x}+\frac{\partial \mathrm{v}}{\partial y}\right) \Delta x \Delta y \Delta t+\frac{\partial u}{\partial x} \frac{\partial \mathrm{v}}{\partial y} \Delta x \Delta y \Delta^2}{\Delta x \Delta y \Delta t}=\frac{\partial u}{\partial x}+\frac{\partial \mathrm{v}}{\partial y}=\theta_x+\theta_y \\ \end{aligned}da$

单位时间单位面积的变化率=两个线变形率之和

2.2角变形速率与旋转角速度

在微分时段内，AB与AC两正交边夹角的变化与微分平面的角变形和转动有关。

在微分时段内，AB边的偏转角度为（逆时针为正)： $\theta_1$ 。由于： $\theta_1$ 为为小量，可以近似： $\theta_1=\frac{B B^{\prime}}{\Delta x}$ 。

同时记AB边的偏转角度为： $\theta_2$ .

$\begin{aligned} & \theta_1=\frac{B B^{\prime}}{\Delta x}=\frac{\left(\mathrm{v}+\frac{\partial \mathrm{v}}{\partial x} \Delta x-\mathrm{v}\right) \Delta t}{\Delta x}=\frac{\partial \mathrm{v}}{\partial x} \Delta t \\ & \theta_2=-\frac{C C^{\prime}}{\Delta y}=-\frac{\left(u+\frac{\partial u}{\partial y} \Delta y-u\right) \Delta t}{\Delta y}=-\frac{\partial u}{\partial y} \Delta t \end{aligned}$

将平面微团夹角的总变化量分解为：角变形运动变化和旋转运动的变化。

设在微分时段内, 平面微团角平分线转动角度为 $\alpha$ , 边线的纯角变形量为 $\beta$ , 则由几何关系可得

$\theta_1=\alpha+\beta \quad \theta_2=\alpha-\beta$

解出可得

$\alpha=\frac{\theta_1+\theta_2}{2} \quad \beta=\frac{\theta_1-\theta_2}{2}$

定义：

平面微团的旋转角速度（单位时间的旋转角度）为：

$\omega_z=\lim _{\Delta t \rightarrow 0} \frac{\alpha}{\Delta t}=\frac{1}{2}\left(\frac{\partial \mathrm{v}}{\partial x}-\frac{\partial u}{\partial y}\right)$

平面微团的角变形速率 (单位时间单边角变形量）为：

$\gamma_z=\lim _{\Delta t \rightarrow 0} \frac{\beta}{\Delta t}=\frac{1}{2}\left(\frac{\partial \mathrm{v}}{\partial x}+\frac{\partial u}{\partial y}\right)$

2.3三维六面体的变形

将上述结论推广到三位六面体的运动，标记其中心点的速度为 $x(u,v,w)$

流体微团线变形速率 $\quad \theta_x=\frac{\partial u}{\partial x}, \theta_y=\frac{\partial v}{\partial y}, \theta_z=\frac{\partial w}{\partial z}$
流体微团角变形速率(剪切变形速率)

$\gamma_x=\frac{1}{2}\left(\frac{\partial w}{\partial y}+\frac{\partial v}{\partial z}\right), \gamma_y=\frac{1}{2}\left(\frac{\partial u}{\partial z}+\frac{\partial w}{\partial x}\right), \gamma_z=\frac{1}{2}\left(\frac{\partial v}{\partial x}+\frac{\partial u}{\partial y}\right)$

流体微团旋转角速度

$\omega_x=\frac{1}{2}\left(\frac{\partial w}{\partial y}-\frac{\partial v}{\partial z}\right), \omega_y=\frac{1}{2}\left(\frac{\partial u}{\partial z}-\frac{\partial w}{\partial x}\right), \omega_z=\frac{1}{2}\left(\frac{\partial v}{\partial x}-\frac{\partial u}{\partial y}\right)$

3.流体微团速度分解定理

在流场中任意两个微距点 $M_0$ 和 $M_1$

$M_0$ 点的速度标记为

$u(x,y,z,t)\\v(x,y,z,t)\\z(x,y,z,t)$

$M_1$ 点的速度标记为

$u(x+\Delta x ,y+ \Delta y,z+ \Delta z,t)\\v(x+\Delta x ,y+ \Delta y,z+ \Delta z,t)\\z(x+\Delta x ,y+ \Delta y,z+ \Delta z,t)$

如何用 $M_0$ 点的速度标记 $M_1$ 点的速度

$u(x+\Delta x ,y+ \Delta y,z+ \Delta z,t)=u(x,y,z,t)+\frac{\partial u}{\partial x}\Delta x+\frac{\partial u}{\partial y}\Delta y+\frac{\partial u}{\partial z}\Delta z\\=u(x,y,z,t)+(w_y\Delta z-w_z\Delta y)+\theta_x\Delta x+\gamma_z\Delta y+\gamma_y\Delta z$

可以看出，一个点的速度可以用另一个点的速度再加上微团的旋转运动、线变形运动和角变形运动。

实际流体微团的运动可以是一种或几种运动的组合。

直匀流动匀速直线运动，流体微团只有平动，无转动和变形运动。
无旋流动，流体微团存在平动、变形运动，但无转动。
旋转容器内的流体运动，流体微团存在平动和转动，但无变形运动。

流体速度分解定理只是对流体微团成立，属于局部性定理。

4.散度及其意义

【散度】：在流体力学里表示流体微团的相对体积膨胀率（单位时间单位体积的增长量）。

三个相互垂直方向的线变形率之和在向量分析中称为速度 $V$ 的散度，符号为 $divV$ ,即

$\operatorname{div} \vec{V}=\nabla \cdot \vec{V}=\frac{\partial u}{\partial x}+\frac{\partial v}{\partial y}+\frac{\partial w}{\partial z}$

含义与推导的说明：

取一简单的矩形微元六面体，原边长为 $\Delta x，\Delta y，\Delta z$ ；则体积为 $(\Delta x\Delta y\Delta z)$

经过 $\Delta t$ 时间之后，边长变化

$\begin{aligned} &\Delta x \rightarrow\left(1+\frac{\partial u}{\partial x} \Delta t\right) \Delta x \quad \Delta y \rightarrow\left(1+\frac{\partial v}{\partial y} \Delta t\right) \Delta y \\ &\Delta z \rightarrow\left(1+\frac{\partial w}{\partial z} \Delta t\right) \Delta z \\ \end{aligned}$

则相对体积的膨胀率（单位时间单位体积的增长量）为：

$\begin{aligned} & \begin{array}{l} d i v \vec{V}=\lim _{\Delta x \rightarrow} \frac{1}{\Delta x \Delta y \Delta z \Delta t}\left[\left(1+\frac{\partial u}{\partial x} \Delta t\right) \Delta x\left(1+\frac{\partial v}{\partial y} \Delta t\right) \Delta y\left(1+\frac{\partial w}{\partial z} \Delta t\right) \Delta z-\Delta x \Delta y \Delta z\right] \\ \quad=\frac{\partial u}{\partial x}+\frac{\partial v}{\partial y}+\frac{\partial w}{\partial z}=\nabla \cdot \vec{V} \end{array} \end{aligned}$

流体微团在运动分析中，若为密度不变的不可压缩流动中，微团体积不变，其速度的散度必为零。

$\operatorname{div} \vec{V}=\nabla \cdot \vec{V}=\frac{\partial u}{\partial x}+\frac{\partial v}{\partial y}+\frac{\partial w}{\partial z}=0$

如果是密度有变化的流动（可压缩流体），那么散度一般不等于零。

5.旋度和速度势函数

5.1旋度

流体微团绕自身轴的旋转角速度的三个分量为 $\omega_x ,\omega_y ,\omega_z$ ，合角速度可用矢量表示为

$\vec{\omega}=\omega_x \vec{i}+\omega_y \vec{j}+\omega_z \vec{k}=\frac{1}{2} r o t \vec{V}=\frac{1}{2} \nabla \times \vec{V}$

这个值在向量分析里记为 $(1/2)rotV$ ，称为速度场的旋度。

【无旋流场】：各处的 $\omega$ 都为 $0$ ，其流动称为无旋流。与其相对的是有旋流场，流动称为涡流。

【斯托克斯定理】： $Stokes$ 定律，速度沿着某一封闭曲线的线积分等于封闭曲线所张开的任意曲面的涡通量（散度与面积的点乘）

$\begin{aligned} & \oint_L \vec{V} \cdot d \vec{r}=\iint_A \operatorname{rot} \vec{V} \cdot d \vec{A} \\ \end{aligned}$

对于无涡流场，由于 $\omega$ 都为 $0$ ，所以其旋度为 $0$ ，

$\quad \oint_L \vec{V} \cdot d \vec{r}=0$

5.2速度势函数

【速度势函数】： $d \phi$

$d \phi=\vec{V} \cdot d \vec{r}=u d x+v d y+w d z \\\quad \oint_L \vec{V} \cdot d \vec{r}=\oint_L d \phi=0$

速度势函数存在的充分必要条件是速度场的旋度等于 $0$ ，即 $\vec{\omega}=\frac{1}{2} r o t \vec{V}=0$

速度势函数是坐标位置和时间的函数， $\phi=\phi(x,y,z,t)$

速度势函数与速度分量的关系：

说明速度势函数在某个方向的偏导数等于速度矢量在那个方向的分量。

$u=\frac{\partial \phi}{\partial x} \quad \quad v=\frac{\partial \phi}{\partial y} \quad \quad w=\frac{\partial \phi}{\partial z}$

对于无旋流，沿一条连接A、B两点的曲线进行速度的线积分，结果只与二端点的 $\phi$ 值之差有关而与积分路径无关。

$\int_{A}^{B}(udx+vdy+wdz)=\int_{A}^{B}d \phi=\phi_B-\phi_A$

第六讲：理想流体运动微分方程组

1.连续性微分方程

连续性方程是质量守恒定律在流体力学中的表现形式。

推导：

在空间中取一个六面体，其边长为 $dx,dy,dz$ 。在 $t$ 时刻，过中心点的流体微团的三个分速度为 $u,v,w$ ，密度是$\rho $，通过单个截面的流量是$ \rho u$。

侧面流入微分六面体的净流体总和质量：

$\begin{aligned} & \Delta m=\Delta m_x+\Delta m_y+\Delta m_z \\ & \quad=-\left[\frac{\partial(\rho u)}{\partial x}+\frac{\partial(\rho v)}{\partial y}+\frac{\partial(\rho w)}{\partial z}\right] d x d y d z d t \\ \end{aligned}$

由于在这一过程中微分六面体的体积不变，故质量的改变只是因为密度的变化
密度$\rho $是空间位置和时间的函数。密度变化引起微分六面体质量的增量表示为：

$\Delta m_t=\left[\rho+\frac{\partial \rho}{\partial t} d t\right] d x d y d z-\rho d x d y d z=\frac{\partial \rho}{\partial t} d x d y d z d t$

根据质量守恒定律，在 $dt$ 时段内从侧面净流入微分六面体的总质量应等于六面体内流体质量因密度随时间变化的引起增量。

$\Delta m=-\left[\frac{\partial(\rho u)}{\partial x}+\frac{\partial(\rho v)}{\partial y}+\frac{\partial(\rho w)}{\partial z}\right] d x d y d z d t=\frac{\partial \rho}{\partial t} \frac{d x d y d z d t}{v}$

整理得到连续性微分方程：

$\begin{aligned} &\frac{\partial \rho}{\partial t}+\frac{\partial(\rho u)}{\partial x}+\frac{\partial(\rho v)}{\partial y}+\frac{\partial(\rho w)}{\partial z}=0 \\ & \frac{\partial \rho}{\partial t}+\nabla \cdot(\rho \vec{V})=0 \\ & \frac{\partial \rho}{\partial t}+u \frac{\partial \rho}{\partial x}+v \frac{\partial \rho}{\partial y}+w \frac{\partial \rho}{\partial z}+\rho\left(\frac{\partial u}{\partial x}+\frac{\partial v}{\partial y}+\frac{\partial w}{\partial z}\right)=0 \\ & \frac{d \rho}{d t}+\rho \nabla \cdot \vec{V}=0(另一种表达形式) \end{aligned}$

【不可压缩流体】： $\frac{d \rho}{d t}=0$ 。是指每个质点的密度在流动过程中保持不变，但是流体质点之间的密度可以不同，因此其密度并不一定处处都是常数对。于不可压缩流体，所以连续方程变为

$\frac{d \rho}{d t}=0 \quad \nabla \cdot \vec{V}=0 \quad \frac{\partial \mathrm{u}}{\partial \mathrm{x}}+\frac{\partial v}{\partial y}+\frac{\partial w}{\partial z}=0$

根据散度的定义（单位体积的净流出量）, 有

$\operatorname{div}(\rho \vec{V})=\nabla \cdot(\rho \vec{V})=\lim _{\tau \rightarrow 0} \frac{\oiint_A(\rho \vec{V}) \cdot \vec{n} d A}{\tau}$

式中： $\tau$ ——表示流出截面的面积
$(\rho \vec{V}) \cdot \vec{n} d A$ ——表示控制面的净流出量

高斯公式：

$\iiint_\tau \nabla \cdot(\rho \vec{V}) d \tau=\oiint_A \vec{n} \cdot(\rho \vec{V}) d A$

【均值流体】： $\nabla\rho =0$ ，密度在空间上的分布是相同的，但是随时间的变化性不能保证。

同时满足不可压缩流体和均值流体，才能得出$\rho=C $为常数的结论

2.Euler运动微分方程组

欧拉运动微分方程组是在不计流体粘性前提下推导出来的，该方程实质上是微分形式的动量方程。

推导：

依旧建立一微分六面体，其边长为 $dx,dy,dz$ 。

设六面体中心点坐标为 $(x,y,z)$ ，相应该点处的流体要素为压强 $p(x,y,z,t)$ ，单位质量力，速度 $u,v,w$ 。
左右两边均受到外界法向力的作用

微元六面体在 $x$ 方向上的质量力： $\rho dxdydzf_x$ ，密度×体积×单位质量力

依据牛顿定律，x方向合外力等于质量乘以x方向加速度

$\left(p-\frac{\partial p}{\partial x} \frac{d x}{2}\right) d y d z-\left(p+\frac{\partial p}{\partial x} \frac{d x}{2}\right) d y d z+\rho f_x d x d y d z=\frac{d u}{d t} \rho d x d y d z$

化简得到 $x$ 方向的运动方程，将三个方向的运动方程组合得到【欧拉运动微分方程组】：

$\begin{aligned} &\frac{d u}{d t}=f_x-\frac{1}{\rho} \frac{\partial p}{\partial x} \\&\frac{d v}{d t}=f_y-\frac{1}{\rho} \frac{\partial p}{\partial y}\\ &\frac{d w}{d t}=f_z-\frac{1}{\rho} \frac{\partial p}{\partial z} \end{aligned}$

【欧拉运动微分方程组的向量形式】：

$\frac{d \vec{V}}{d t}=\vec{f}-\frac{1}{\rho} \nabla p$

得到加速度产生的根本原因就是质量力与表面力的差值（压力梯度）。

$\begin{aligned} & \frac{du}{dt}(加速度)>0, f_x-\frac{1}{\rho} \frac{\partial p}{\partial x}>0 \text {, 收缩通道, } \frac{\partial p}{\partial x}<\rho f_x \\ & \frac{du}{dt}(加速度)=0, f_x-\frac{1}{\rho} \frac{\partial p}{\partial x}=0 \text {, 等截面通道, } \frac{\partial p}{\partial x}=\rho f_x \\ & \frac{du}{dt}(加速度)<0, f_x-\frac{1}{\rho} \frac{\partial p}{\partial x}<0 \text {, 扩张通道, } \frac{\partial p}{\partial x}>\rho f_x \\ \end{aligned}$

【欧拉运动微分方程组的加速度表示】：

$\begin{aligned} & \frac{\partial u}{\partial t}+u \frac{\partial u}{\partial x}+v \frac{\partial u}{\partial y}+w \frac{\partial u}{\partial z}=f_x-\frac{1}{\rho} \frac{\partial p}{\partial x} \\ & \frac{\partial v}{\partial t}+u \frac{\partial v}{\partial x}+v \frac{\partial v}{\partial y}+w \frac{\partial v}{\partial z}=f_y-\frac{1}{\rho} \frac{\partial p}{\partial y} \\ & \frac{\partial w}{\partial t}+u \frac{\partial w}{\partial x}+v \frac{\partial w}{\partial y}+w \frac{\partial w}{\partial z}=f_z-\frac{1}{\rho} \frac{\partial p}{\partial z} \\ \end{aligned}$

【欧拉运动微分方程组的加速度式的向量表示】：

$\begin{aligned} \frac{\partial \vec{V}}{\partial t}+(\vec{V} \cdot \nabla) \vec{V}=\vec{f}-\frac{1}{\rho} \nabla p \end{aligned}$

3.Bernoulli积分及其物理意义

欧拉运动微分方程组的加速度表示中，在加速度项中显示出旋转角度。
导出了【格罗米柯—Lamb型方程】：

$\begin{aligned} & u \frac{\partial u}{\partial x}+v \frac{\partial u}{\partial y}+w \frac{\partial u}{\partial z} \\ & =u \frac{\partial u}{\partial x}+v \frac{\partial v}{\partial x}+w \frac{\partial w}{\partial x}-v\left(\frac{\partial v}{\partial x}-\frac{\partial u}{\partial y}\right)+w\left(\frac{\partial u}{\partial z}-\frac{\partial w}{\partial x}\right) \\ & =\frac{\partial}{\partial x}\left(\frac{V^2}{2}\right)-2 v \omega_z+2 w \omega_y \\ \end{aligned}$

【矢量形式】：

$\vec{f}-\frac{1}{\rho} \nabla p-\nabla\left(\frac{V^2}{2}\right)=\frac{\partial \vec{V}}{\partial t}-2 \vec{V} \times \vec{\omega}$

对于理想正压流体，在质量力有势条件下，假设为定常流动，可以得到

有势—质量力存在一个临时函数【 $\vec{f}=-\nabla \Pi$ 】；理想正压流体—密度仅为压强的函数， $\frac{1}{\rho}dp$ 可积【 $\nabla P=\frac{1}{\rho} \nabla p$ 】；定常流动—【$\frac{\partial \vec{V}}{\partial t}=0 $】

格罗米柯方程变为：

$-\nabla \Pi-\nabla P-\nabla(\frac{V^2}{2})=-2 \vec{V} \times \vec{\omega} \quad$

$\begin{aligned} \nabla\left(\Pi+P+\frac{V^2}{2}\right)=2 \vec{V} \times \vec{\omega} \\ \end{aligned}$

现在流场中，任取一条光滑曲线，并将上式投影到曲线上，有

$\frac{\partial}{\partial s}\left(\Pi+P+\frac{V^2}{2}\right) d s=2 \vec{V} \times \vec{\omega} \cdot d \vec{s}$

如果上式右边项为零，有 $\vec{V} \times \vec{\omega} \cdot d \vec{s}=0$

即可得到， $\frac{\partial}{\partial s}\left(\Pi+P+\frac{V^2}{2}\right)=0 \quad \quad \Pi+P+\frac{V^2}{2}=C(s)$

这就是Bernoulli积分，或伯努利方程。上式表明，==对于理想正压流体的定常流动，在质量力有势条件下，单位体积流体微团沿着这条特定曲线s的势能、压能和动能之和不变，即总机械能不变==。

伯努利积分成立的条件： $\vec{V} \times \vec{\omega} \cdot d \vec{s}=0$

沿任意一条流线，可以成立：

$\vec{ds}//\vec{V}\quad \quad \vec{V}\times \vec{w}\perp \vec{V}\quad \quad\vec{V} \times \vec{\omega} \cdot d \vec{s}=0$

沿任意的涡线成立：

$\vec{ds}//\vec{w}\quad \quad \vec{V}\times \vec{w}\perp \vec{w}\quad \quad\vec{V} \times \vec{\omega} \cdot d \vec{s}=0$

满足： $\vec{V} \times \vec{\omega}=0$

静止流场， $\vec{V} =0$
无旋流场，有势流动。 $\vec{\omega}=0$
流线与涡线重合，即螺旋流动。 $\vec{V} //\vec{\omega}$

对于不可压缩流体，在不计质量力情况下：

Bernoulli积分变为 $\frac{p}{\rho}+\frac{V^2}{2}=C(s)$
如果质量力只有重力, bernoulli积分变为 $g z+\frac{p}{\rho}+\frac{V^2}{2}=C(s)$

又可以整理为：

$z+\frac{p}{\gamma }+\frac{V^2}{2g}=H(s)$

上式表示不可压缩流体，在质量力为重力作用下的能量方程。
表明，沿任意一条流线，==单位重量流体所具有的势能、压能和动能之和不变==。

式中： $z$ ——表示单位重量流体相对于基准面高度，称为位置水头；
$\frac{p}{\gamma }$ ——表示单位重量流体在绝对真空管中上升的高度，称为压强水头；
$\frac{V^2}{2g}$ ——表示单位重量流体垂直上抛所能达到高度，称为速度水头；
$H$ ——表示沿流线单位重量流体具有的总能量，称总水头。

流体质点运动中，动能、压能、势能之间可以相互转化。

4.Bernoulli方程应用

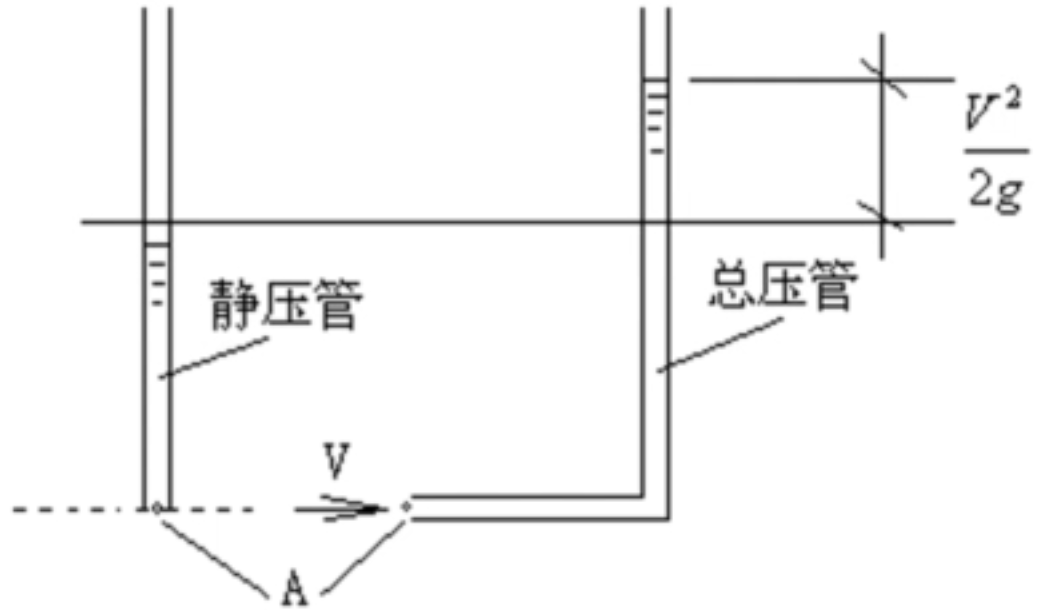
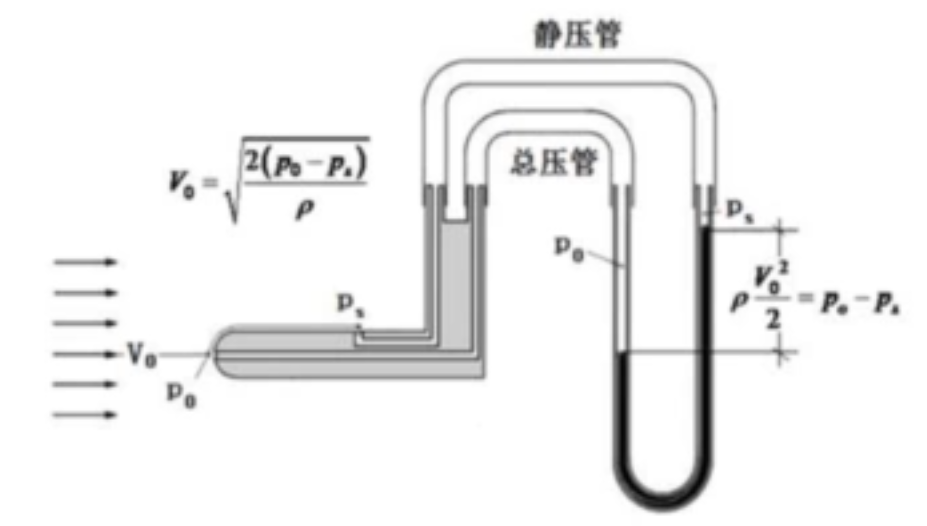
两管封装就形成了空速管。
总压孔对准来流，来流撞在孔上速度降为零，相应的压强达到了总压p，而静压孔处感受到的是静压。
两者之差恰好为一个速度水头。

皮托管测速原理普朗特的风速管

第七讲：流体（空气）运动积分方程

1.系统与控制体的定义

流体运动积分方程包括：连续性方程、动量方程、动量矩方程、能量方程

【系统】：在流体力学中，系统是指由任何确定流体质点组成的质团。

【控制体】：被流体所流过，相对于坐标系而言，固定不变的任何体积称为控制体。
控制体的边界，称为控制面。控制体是不变的，但占据控制体的流体质点随时间是变化的。

2.Lagrange型积分方程

连续方程：（质量守恒）表示，在系统内不存在源和汇的情况下，系统的质量不随时间变化。

$p_0=\rho g\left(y+\frac{V^2}{2 g}\right) \quad p_0=\rho g y \quad V=\sqrt{\frac{2\left(p_0-p_0\right)}{\rho}} \frac{d M}{d t}=\frac{d}{d t} \iiint_{r_0} \rho d \tau=\mathbf{0}$

**动量方程：**系统的动量对时间的变化率等于外界作用于系统上的所有外力的合力。

$\frac{d \vec{K}}{d t}=\frac{d}{d t} \iiint_{\tau_0} \rho \vec{V} d \tau_0=\Sigma \overrightarrow{\boldsymbol{F}}=\iiint_{\tau_0} \rho \vec{f} d \tau_0+\iint_{S_0} \overrightarrow{p_n} d \boldsymbol{S}$

**动量矩方程：**系统对某点的动量矩对时间的变化率等于外界作用于系统上所有外对同一点力矩之和。

$\frac{d \vec{M}_r}{d t}=\frac{d}{d t} \iiint_{\tau_0} \rho \vec{r} \times \vec{V} d \tau_0=\Sigma \vec{r} \times \vec{F}=\iiint_{\tau_0} \rho(\vec{r} \times \vec{f}) d \tau_0+\oiint \int_{S_0} \vec{r} \times \overrightarrow{p_n} d S_0$

**能量方程：**单位时间内由外界传入系统的热量Q与外界对系统所做的功W之和等于该系统的总能量E对时间的变化率。

$\begin{aligned} Q+\boldsymbol{W}=\frac{d \boldsymbol{E}}{d t}=\frac{d}{d t} \iiint_{\tau_0} \rho\left(\mathrm{e}+\frac{V^2}{2}\right) d \tau_0 \\ \end{aligned}$

3.Reynolds输运方程

对于Lagrange型积分方程的改写，为使其更加适用于控制体的形式。引入随体导数$\sigma $

$I=\int \int \int _{\tau _{0}}\rho \sigma d\tau _{0}$

当$\sigma=1 $时，$ I=M$代表系统的质量；

当$\sigma= \vec{V} $时，$ I=K$代表系统的动量；

当$\sigma=\vec{r}\times \vec{V} $时，$ I=M_r$代表系统的动量矩；

当$\sigma=e+\frac{V^2}{2} $时，$ I=E$代表系统的能量。

Reynolds输运方程：

$\begin{aligned} \frac{dI}{d t}=\frac{d}{d t} \iiint_{\tau_0} \rho \sigma d \tau_\sigma &=\iiint_{\tau_0}\frac{\partial\rho \sigma}{\partial t}d\tau + \oiint_S\rho \sigma(\vec{V}\cdot \vec{n})dS\\&=\frac{\partial}{\partial t}\iiint_{\tau_0}\rho \sigma d\tau + \oiint_S\rho \sigma(\vec{V}\cdot \vec{n})dS \end{aligned}$

式中： $\frac{dI}{d t}$ 等于系统的总的积分量随时间的变化率，也表示所引入的随体导数；
$\iiint_{\tau_0}\frac{\partial\rho \sigma}{\partial t}d\tau$ ——控制体内物理量随时间的偏导数；
$\oiint_S\rho \sigma(\vec{V}\cdot \vec{n})dS$ ——通过控制面的净流出量。

第一部分表示控制体内物理量随时间的变化率，表征了流场的非定常特性。

第二部分表示单位时间内，通过控制面流出物理量的净增量，是由于流场的不均匀性引起的。

综合起来，表示系统的随体导数等于单位时间内控制体内物理量随时间引起的增量与通过控制面流出物理量的净增量之和。

4.Euler型积分方程

Euler型积分方程是对控制体建立的积分方程。在Reynolds输运方程的基础上，可以得到以下结论。

连续方程（质量守恒）：

取 $\sigma =1$ ，得到连续方程：

$\frac{dM}{d t}=\frac{d}{d t} \iiint_{\tau_0} \rho d \tau_\sigma =\frac{\partial}{\partial t}\iiint_{\tau_0}\rho d\tau + \oiint_S\rho (\vec{V}\cdot \vec{n})dS=0$

方程的物理含义：在控制体内无源和汇的情况下，单位时间内从控制体流出的质量等于控制体内质量的减小量。

动量方程：

当$\sigma= \vec{V} $时，

$\begin{aligned} & \frac{d \vec{K}}{d t}=\frac{d}{d t} \iiint_{\tau_0} \rho \vec{V} d \tau_0=\Sigma \vec{F} \\ & \frac{\partial}{\partial t} \iiint_\tau \rho \vec{V} d \tau+\oiint_S \rho \vec{V}(\vec{V} \bullet \vec{n}) d S=\iiint_\tau \rho \vec{f} d \tau+ \oiint_S \vec{p}_n d S \\ \end{aligned}$

方程的物理含义：单位时间内，在控制体内动量的增量加上通过控制面流出的净动量等于外界作用于控制体上所有外力（质量力和表面力）之和。

动量矩方程：

当$\sigma=\vec{r}\times \vec{V} $时，

$\begin{aligned} & \frac{d \vec{M}_r}{d t}=\frac{d}{d t} \iiint_{T_0} \rho \vec{r} \times \vec{V} d \tau_0=\frac{\partial}{\partial t} \iiint_\tau \rho \vec{r} \times \vec{V} d \tau+\oiint \oiint_S \rho \vec{r} \times \vec{V}(\vec{V} \bullet \vec{n}) d S \\ & =\Sigma \vec{r} \times \overrightarrow{\boldsymbol{F}}=\iiint_\tau \rho(\vec{r} \times \vec{f}) d \tau+\oiint_S \vec{r} \times \overrightarrow{p_n} d S \\ \end{aligned}$

方程的物理含义：单位时间内，控制体内动量矩的增量加上通过控制面流出的净动量矩等于外界作用于控制体上所有外力矩（质量力矩和表面力矩）之和。

能量方程：

当$\sigma=e+\frac{V^2}{2} $时，

$\begin{aligned} & \frac{d}{d t} \iiint_{\tau_0} \rho\left(\mathrm{e}+\frac{V^2}{2}\right) d \tau_0 \\ & =\frac{\partial}{\partial t} \iiint_\tau \rho\left(\mathrm{e}+\frac{V^2}{2}\right) d \tau+\oiint_S \rho\left(e+\frac{V^2}{2}\right)(\vec{V} \bullet \vec{n}) d S \\ & =\oiint_S q_\lambda d S+\iiint_\tau \rho q_R d \tau+\iiint_\tau \rho \vec{f} \bullet \vec{V} d \tau+\oiint_S \overrightarrow{p_n} \bullet \vec{V} d S \\ \end{aligned}$

方程的物理含义：单位时间内，控制体内总能量的增量加上通过控制面流出的净总能量等于传给控制体内流体的热量（热传导量、热辐射量）加上所有力（质量力、表面力）对控制体内流体所做的功。

【质量力】：质量力是某种力场作用在全部流体质点上的力，其大小和流体的质量或体积成正比。在生活中，我们常见的质量力是重力 $G=mg$ 、直线运动惯性力 $F=ma$ 、离心惯性力 $F_c=m*r*w^2$ 。

【有势质量力】：质量力所做的功只与起点和终点的位置有关,这样的质量力称为有势质量力。

有势—质量力存在一个临时函数【 $\vec{f}=-\nabla \Pi$ 】

对于理想流体、质量力有势、绝热定常流动，简化能量方程。

$\begin{aligned} \iiint_\tau \rho \vec{f} \bullet \vec{V} d \tau&=-\iiint_\tau \rho \nabla \Pi \bullet \vec{V} d \tau=-\iiint_\tau \nabla \bullet(\Pi \rho \vec{V}) d \tau+\iiint_\tau \Pi \nabla \bullet(\rho \vec{V}) d \tau \\ & =-\iiint_\tau \nabla \bullet(\Pi \rho \vec{V}) d \tau=-\oiint_S \vec{n} \bullet(\Pi \rho \vec{V}) d S \\ \end{aligned}$

5.应用举例

有一种尾迹测阻法，可以用来测量一个二维物体的型阻（型阻是由粘性直接间接造成的物体阻力）。

通过风洞产生的流场，利用毕托管测出翼型来流和下游出流的速度分布，由速度分布的积分得到气流对翼型的阻力

在翼型上、下游断面间建立一个控制体，控制体两侧边是流线，控制体上、下游断面的高度是 $h_1,h_2$ ，控制体入流速度是$V_\infty $（均匀），控制体出流速度是$ u_2 $（沿Y向有不同分布），气流对翼型的阻力是$ D$（沿X方向）

控制体上面的连续方程和动量方程的表达：

$\int_0^{h_1} \rho V_{\infty} d y=\int_0^{h_2} \rho u_2 d y\\D=\int_0^{h_2} \rho u_2^2 d y-\int_0^{h_1} \rho V_{\infty}^2 d y$

上游1断面流入质量=下游2断面流出质量
阻力=出流动量—流入动量

两式结合推导：

$\begin{aligned} & D=V_{\infty} \int_0^{h_1} \rho V_{\infty} d y-\int_0^{h_2} \rho u_2^2 d y \\ & =V_{\infty} \int_0^{h_2} \rho u_2 d y-\int_0^{h_2} \rho u_2^2 d y \\ & =\int_0^{h_2} \rho u_2\left(V_{\infty}-u_2\right) d y \\ & \end{aligned}$

第八讲：流体的漩涡运动

1.自然和工程界中的旋涡运动

自然界中典型的漩涡运动：龙卷风

工程中：飞机在飞行中产生的翼梢涡

理论：二维圆柱绕流的卡门涡街

2.旋涡、涡量涡通量、环量的基本概念

【旋涡】：是指一群绕公共中心轴旋转的流体质团的运动。

旋涡的强弱正比于微团的旋转角速度和旋转区域的面积的乘积。

漩涡的结构：柱状涡、螺旋涡、圆盘涡(环状)

涡心速度：由于热气流上升运动，速度也是随之向上的；由于冷气流下沉运动，速度也是随之向下的。

【旋度】$\nabla $：旋度是向量分析中的一个向量算子，可以表示三维向量场对某一点附近的微元造成的旋转程度。
速度场的旋度其数学表示可以记为：

$\begin{aligned} & r o t \vec{V}=2 \vec{\omega}=\nabla \times \vec{V}=\left[\begin{array}{ccc} \vec{i} & \overrightarrow{\mathrm{j}} & \overrightarrow{\mathbf{k}} \\ \frac{\partial}{\partial x} & \frac{\partial}{\partial y} & \frac{\partial}{\partial z} \\ u & \mathbf{v} & \mathbf{w} \end{array}\right] \\ \end{aligned}$

【涡量】 $\Omega_ z$ ：涡量是指流场中任何一微团旋转角速度的2倍，它是一个纯运动学的概念，也是速度场的旋度。
涡旋通常用涡量来量度其强度和方向

对于二维流动，涡量为： $\Omega_ z =2\omega _{z}$
对于三维流动，流体微团有三个方向的角速度则合角速度为：

$\begin{aligned} & \vec{\omega}=\omega_x \vec{i}+\omega_y \vec{j}+\omega_z \vec{k} \quad|\vec{s}|=\sqrt{\Omega_x^2+\Omega_y^2+\Omega_z^2} \\ & \vec{\Omega}=\mathbf{2} \vec{\omega} \\ \end{aligned}$

【涡线】：涡线像流线一样，在同一瞬时，如在涡量场中存在一条曲线其上每一点的涡量方向都与该线相切，这条曲线叫涡线。
涡线的微分方程：

$d\vec{r}\propto \vec{\Omega }\\\frac{dx}{\Omega _{x}}，\frac{dy}{\Omega _{y}}，\frac{dz}{\Omega _{z}}$

【涡面】：涡面给定瞬间，通过某一曲线（本身不是涡线)的所有涡线构成的曲面称为涡面。

【涡管】：由封闭涡面组成的管状涡面称为涡管。

【涡通量】 $I$ ：涡量与旋转区域面积的乘积，也称为涡通量，也称为涡强。

如果涡量分布均匀，涡量和涡通量（涡强度）为： $\Omega _z =2\omega _{z}$ ， $I=\Omega _z A$
如果涡量分布不均匀 $\Omega _z =2\omega _{z}=f(x,y)$ ，那必须对涡量进行面积积分来表达。

$I=\iint_A \Omega_z d x d y=\iint_A f(x, y) d x d y$

在旋转区域内，涡量的平均值也是一个特征量，表示为： $\Omega_{z a}=2 \omega_a=\frac{I}{A}=\frac{\iint_A \Omega_z d x d y}{A}$ 。

对于任意空间曲面，涡通量可表示为

$\iint_S 2 \vec{\omega} \cdot d \vec{S}=\iint_S 2 \omega \cos \gamma d S I=\iint_S \vec{\Omega} \bullet d \vec{S}$

式中： $S$ ——任意形状空间曲面；
$\gamma$ ——曲面上的微元面积 $dS$ 的法线和$\omega $的轴线之间的夹角。

【速度环量】 $\Gamma$ ：

对于二维流场，如果涡量分布均匀，通过半径为R的圆内的涡通量可以表示为圆周切向速度的线积分。

引出速度环量的定义：对于任意速度场 $V$ ，沿空间任意取一封闭曲线 $L$ ，则速度矢量在此封闭曲线上的线积分称为速度环量。
速度环量的值与绕行方向有关，约定以逆时针绕行为正。

【斯托克斯定理】：对于流场中，沿任意空间封闭曲线L的速度环量等于穿过张在L上任意曲面S上的涡通量，这个通量值与所张的曲面形状无关，只跟围线所包含的涡量有关。

$\Gamma=\oint_L \vec{V} \cdot d \vec{S}=\iint_S 2 \vec{\omega} \cdot d \vec{S}=\iint_S r o t \vec{V} \cdot d \vec{S}$

3.涡的诱导速度

一条强度为 $Γ$ 的涡线，一段 $ds$ 对线外的一点 $P$ 会产生一个诱导速度，情况正像电流会产生磁力的一样。
表达涡段所产生的诱导速度的公式是，毕奥-萨瓦公式：

$d V=\frac{\Gamma d s}{4 \pi r^2} \sin \theta \quad d \vec{V}=\frac{\Gamma}{4 \pi} \frac{d \vec{s} \times \vec{r}}{r^3}$

式中： $Γ$ ——涡线的强度；
$r$ ——涡线和诱导点的距离；
$\theta $——涡线和诱导点之间的夹角

==对于该定理的引申在《南航—空气动力学》第二讲3.1中有过记录，此处将借用当时的笔记。==

4.理想流中的涡定理

对于理想正压流体，在质量力有势条件下，关于涡量场的Helmholtz.三大定理：

定理1：在某一时刻沿涡线或涡管的涡强不变（或涡强保持定理)
这就是说沿涡管，不论在什么地方计算它的环量（涡强），其值都是相同的。

定理一的推广：一根涡管在流体里不可能中断，可以伸展到无限远去，可以自相连接成一个涡环（不一定是圆环），也可以止于边界，固体的边界或自由边界（如自由液面）。

定理2：在某时刻构成涡线和涡管的流体质点，在以后运动过程仍将构成涡线和涡管。（涡线保持定理）
说明涡线和涡管随着构成它的流体质点一起运动。
定理3：在理想流中涡的强度不随时间变化，既不会增强，也不会削弱或消失（涡强守恒定律）。

上述三大定理说明：
对于理想正压流体，在质量力有势条件下，流体的涡旋运动既不能产生，也不能消亡。
也就是说，有旋运动永远保持有旋，无旋运动永远保持无旋。

质量力无势（葛氏加速度），非正压流体，流体的粘性是产生涡、消亡涡、改变涡强的重要原因。

【正压流体】：流体内部任一点的压力只是密度的函数的流体。
【非正压流体】：流体内部任一点的压力除与密度有关还与温度有关的流体。

第九讲：理想不可压缩流体的平面势流

1.理想不可压缩流体平面势流的基本方程

对于理想不可压缩流体，流动的基本方程是连续性微分方程和欧拉运动微分方程组。
由于压强和速度的耦连和飞行器复杂的实际外形，控制方程的精确解难以获得。

1.1不可压缩理想流体无旋流动的基本方程

连续性微分方程和欧拉运动微分方程组+初始条件（ $t=t_0$ 给定速度场和压强场）+边界条件（势流满足不穿透条件，垂直物面法相速度为零；无穷远处来流速度无穷大）
构成不可压缩势流流动的定解问题。

对于该方程的简化，分解速度和压强的耦合问题。
根据纯运动学方程求出速度势函数和速度分量，再由Bernoulli方程确定流场中各点的压强。

在无旋流动中存在一个速度势函数：

$\vec{V}=\triangledown\phi\quad \quad u=\frac{\partial \phi}{\partial x} \quad \quad v=\frac{\partial \phi}{\partial y} \quad \quad w=\frac{\partial \phi}{\partial z}$

配合连续性微分方程：

$\nabla \cdot \vec{V}=\nabla \cdot \nabla \varphi=0 \\ \frac{\partial u}{\partial x}+\frac{\partial \mathbf{v}}{\partial y}+\frac{\partial w}{\partial z}=0$

求出一个二阶线性齐次偏微分方程——拉普拉斯方程的解

$\frac{\partial^2 \varphi}{\partial x^2}+\frac{\partial^2 \varphi}{\partial y^2}+\frac{\partial^2 \varphi}{\partial z^2}=0$

这个方程完全表征了运动学条件而与动力行为没有关系。

借助伯努力方程联合速度场，得到压强场。

对于理想不可压缩流体，在质量力有势条件下，对于无旋流动运动方程的积分形式为

$\frac{\partial \varphi}{\partial t}+\frac{V^2}{2}+\frac{p}{\rho}+\Pi=C(t)$

其中，第一项为速度势函数对于时间的偏导数，第二项表征动能，第三项表征压能，第四项是质量力的势函数

对于该式，定常流动，质量力只有重力，得到$ \frac{V^2}{2}+\frac{p}{\rho}+g z=C $

进一步，如果忽略质量力（在空气动力学中经常不考虑重力的作用） $\frac{V^2}{2}+\frac{p}{\rho}=C$

再通过伯努力条件求解压强场。

总结：针对欧拉方程组的求解最简单的情况和无旋流动的理想不可压缩平面势流。
综合起来对于理想不可压缩流体无旋流动，控制方程及其初边界条件为：运动学拉普拉斯方程和动力学行为的伯努力积分

$\begin{aligned} & \frac{\partial^2 \varphi}{\partial x^2}+\frac{\partial^2 \varphi}{\partial y^2}+\frac{\partial^2 \varphi}{\partial z^2}=0 \\ & \frac{\partial \varphi}{\partial t}+\frac{V^2}{2}+\frac{p}{\rho}+\Pi=C(t) \\ \end{aligned}$

1.2速度势函数的性质

速度势函数沿着某一方向的偏导数等于该方向的速度分量。
速度势函数的增值方向是沿着流线的方向。
速度势函数满足线性叠加原理，同时满足拉普拉斯方程。因而，其线性叠加也满足拉普拉斯方程。
速度势函数相等的点连成的线称为等势线，速度方向垂直于等势线。

$d \varphi=\mathbf{0} \quad d \varphi=\vec{V} \cdot d \vec{s}=\mathbf{0} \quad \overrightarrow{\mathbf{V}} \perp \mathbf{d} \overrightarrow{\mathbf{s}}$

连接任意两点的速度曲线等于该两点的速度势函数之差。速度线积分与路径无关，仅决定于两点的位置

$\begin{aligned} \int_A^B \vec{V} \cdot d \vec{s}& =\int_A^B(u d x+v d y+w d z) \\ & =\int_A^B\left(\frac{\partial \varphi}{\partial x} d x+\frac{\partial \varphi}{\partial y} d y+\frac{\partial \varphi}{\partial z} d z\right)=\int_A^B d \varphi=\varphi_B-\varphi_A \\ \end{aligned}$

1.3流函数及其性质

【流函数】：满足连续方程的一个描述流速场的标量函数。

推导中需要用到格林公式（变形），

$\oint_L-v d x+u d y=\iint_\sigma\left(\frac{\partial u}{\partial x}+\frac{\partial v}{\partial y}\right) d x d y$

存在该式成立的充要条件： $\frac{\partial u}{\partial x} +\frac{\partial v}{\partial y}=0$

$d \psi=-v d x+u d y \quad \frac{\partial \psi}{\partial \mathrm{x}} d x+\frac{\partial \psi}{\partial y} d y=-v d x+u d y \\ u=\frac{\partial \psi}{\partial y} \quad v=-\frac{\partial \psi}{\partial \mathrm{x}}$

流函数的性质：

流函数值可以差任意常数而不影响流动；
流函数值相等的点的连线是流线。即等流函数线的切线方向与速度矢量方向重合。
流函数在某一方向的偏导数顺时针旋转90°等于该方向的速度。

【满足拉普拉斯方程】：既满足带有拉普拉斯算子形式的方程。
例如： $\triangledown u= \frac{\partial u}{\partial x}+ \frac{\partial u}{\partial y}+ \frac{\partial u}{\partial z}=0$

理想不可压缩流体平面势流，流函数满足拉普拉斯方程。

$\omega_2=\frac{1}{2}\left(\frac{\partial v}{\partial x}-\frac{\partial u}{\partial y}\right)=\frac{1}{2}\left(\frac{\partial}{\partial x}\left(-\frac{\partial \psi}{\partial x}\right)-\frac{\partial}{\partial y}\left(\frac{\partial \psi}{\partial y}\right)\right)=-\frac{1}{2}\left(\frac{\partial^2 \psi}{\partial x^2}+\frac{\partial^2 \psi}{\partial y^2}\right)=0$

过同一点的等速度势函数线与等流函数线正交（等势线与流线正交）

1.4流网及其特征

【流网】：在理想不可压缩流体定常平面势流中，每一点均存在速度势函数和流函数值。
这样在流场中存在两族曲线，一族为流线，另一族为等势线且彼此相互正交。把由这种正交曲线构成的网格叫做流网。

在流网中，每一个网格的边长之比等于势函数和流函数的增值之比。
流网不仅可以显示流速的分布情况，也可以反映速度的大小。如流线密的地方流速大，流线稀疏的地方流速小。

2.理想不可压缩流体平面定常无旋流动数学问题的提法

设给定一平面物体C，无穷远为直均流，在绕流物体不脱体的情况下，求这个绕流问题。

以速度势函数为未知函数的提法

$\frac{\partial^2 \varphi}{\partial x^2}+\frac{\partial^2 \varphi}{\partial y^2}=\left.0 \quad \frac{\partial \varphi}{\partial n}\right|_C=0 \quad \frac{\partial \varphi}{\partial x}=u_{\infty} \quad \frac{\partial \varphi}{\partial y}=v_{\infty}$

以流函数为未知函数的提法

$\frac{\partial^2 \psi}{\partial x^2}+\frac{\partial^2 \psi}{\partial y^2}=0 \quad \psi_C=0 \quad \frac{\partial \psi}{\partial x}=-v_{\infty} \quad \frac{\partial \psi}{\partial y}=u_{\infty}$

以复位势w(z)为未知函数提法

$w(z)=\psi+i\phi$

3.典型奇势流解

3.1直匀流势流解

直匀流是一种速度不变的最简单的平行流动。

其流速表示： $u=a \quad v=b$

流函数：

$\begin{aligned} u&=\frac{\partial \varphi}{\partial x} =a \quad v=\frac{\partial \varphi}{\partial y} =b\\ d \varphi&=\frac{\partial \varphi}{\partial x}dx+\frac{\partial \varphi}{\partial y}dy=adx+bdy\\ \varphi&=ax+by+c \end{aligned}$

势函数：

$\begin{aligned} u&=\frac{\partial \psi}{\partial x} =a \quad v=\frac{\partial \psi}{\partial y} =b\\ d \psi&=\frac{\partial \psi}{\partial x}dx+\frac{\partial \psi}{\partial y}dy=-vdx+udy\\ \psi&=-ax+by+c \end{aligned}$

3.2点源势流解

【源和汇】：源为正、汇为负。设正源是从流场上某一点有一定的流向四面八方流开去的一种流动。负源（又名汇）是一种正源流向相反的向心流动。

对于源由于只向外流动，故 $v_r$ 存在，而 $v_\theta$ 不存在
设半径为r处的流速是 $v_r$ ，那么这个源的总流量是

$Q=2\pi rv_r \quad v_r=\frac{Q}{2\pi}\frac{1}{r}$

这个公式也间接表明了，离源点越远，源影响的速度就越小

为了方便表示流函数和势函数，此处引入极坐标下的速度分量与流函数和势函数偏导数关系。

速度势函数在极坐标下和速度的关系：
【速度势函数在某个方向的偏导数等于速度矢量在那个方向的分量】

$V_r=\frac{\partial \varphi}{\partial r} \quad V_\theta=\frac{1}{r} \frac{\partial \varphi}{\partial \theta} \\$

【任一点流函数沿着某一方向的偏导数等于沿着该方向顺时针旋转90°方向的速度矢量】

$V_r=\frac{1}{r} \frac{\partial \psi}{\partial \theta} \quad V_\theta=-\frac{\partial \psi}{\partial r}$

势函数函数从 $v_r$ 的式子积分得到：

$\varphi=\frac{Q}{2\pi}lnr$

流函数的表达式：

$\psi=\frac{Q}{2\pi}\theta\quad\quad\psi=\frac{Q}{2\pi}arctg\frac{y}{x}$

式中： $Q$ ——表示源的强度（类似于涡通量的表达）

3.3偶极子势流解

等强度的一个源和一个汇，放在 $x$ 轴线上，源放在 $(-h,0)$ 处，汇放在 $(0,0)$ 处。从源出来的流量都进入汇。

速度势函数：

$\varphi=\frac{Q}{2 \pi}\left[\ln \sqrt{(x+h)^2+y^2}-\ln \sqrt{x^2+y^2}\right] \quad$

流函数：

$\psi=\frac{Q}{2 \pi}\left(\theta_1-\theta_2\right)$

其中，$ \theta_1=\operatorname{arctg} \frac{y}{x+h} \quad \theta_2=\operatorname{arctg} \frac{y}{x} $

当→0，但同时Q增大，使 $\frac{Qh}{2\pi}=M$ 。 $M$ 为非零不定量，可以表示偶极子强度。
当速度势函数中h的取值接近极限情况，速度势函数可以改写为：

$\phi(x, y)=\frac{Q}{4 \pi} \lim _{h \rightarrow 0}\left[\ln \frac{x^2+y^2+2 x h+h^2}{x^2+y^2}\right] \\ =\frac{Q}{4 \pi} \lim _{h \rightarrow 0} \frac{2 h x}{x^2+y^2}=M \frac{x}{x^2+y^2}$