一、Design Expert与响应面优化

1.1总体介绍

Design Expert是什么：

Design-Expert由 Stat-Ease 公司开发，是一款专用于执行实验设计（DOE）的软件。Design-Expert提供比较测试，筛选，表征，优化，稳健的参数设计，混合物设计和组合设计。使用简单易于操作，不需数理统计功底，就可以用设计出高效的试验方案，并对实验数据做专业的分析，给出全面、可视化的模型以及优化结果。

响应面优化实验是什么：

在多因素数量处理试验的分析中，可以分析试验指标（因变量）与多个试验因素（自变量）间的回归关系，这种回归可能是曲线或曲面的关系，因而称为响应面分析。在响应面分析中，首先要得到回归方程，然后通过对自变量的合理取值，求得最优值，这就是响应面分析的目的。

响应面优化法，即响应曲面法。这是一种实验条件寻优的方法，适宜于解决非线性数据处理的相关问题。它囊括了试验设计、建模、检验模型的合适性、寻求最佳组合条件等众多试验和计技术；通过对过程的回归拟合和响应曲面、等高线的绘制、可方便地求出相应于各因素水平的响应值。在各因素水平的响应值的基础上，可以找出预测的响应最优值以及相应的实验条件。

可以进行响应面分析的实验设计有多种，但最常用的是下面两种：Central Composite Design-响应面优化分析（CCD）、Box-Behnken Design-响应面优化分析（BBD）。CCD适用于多因素多水平实验，有连续变量存在；BBD适用于因素水平较少（因素一般少于5个，水平为3个）。同时，CCD比BBD实验能更好的拟合相应曲面。

响应面实验优点：

  • 计算简单，考虑随机误差：
    响应面优化法，考虑了试验随机误差；同时，响应面法将复杂的未知的函数关系在小区域内用简单的一次或二次多项式模型来拟合，计算比较简便，是解决实际问题的有效手段。

  • 连续的预测模型：
    所获得的预测模型是连续的，与正交实验相比，其优势是：在实验条件寻优过程中，可以连续的对实验的各个水平进行分析，而正交实验只能对一个个孤立的实验点进行分析。

Design Expert与响应面分析：

Design-Expert 是一款专业的试验设计软件工具，在已经发表的有关响应面（RSM）优化试验的论文中，Design-Expert是使用最广泛的软件。

1.2实验方法与软件操作

实验设置时需要在文章中说明：

  1. 响应面试验的因素和水平
  2. CCD设计表及模拟结果
  3. 回归方程的方差分析
  4. 相关响应面图以及其他图

初始界面New Design，创建新实验。

  • BBD实验设置：

进入软件Response Surface，选择响应面分析Box-Behnken Design，设置窗口如下

Box-Behnken Design

注：其中Blocks表示设计实验的平行组数

点击Next跳转至响应值设计

响应值设计

  • 生成实验组表格：

点击Finish，跳转至设置出的实验表格

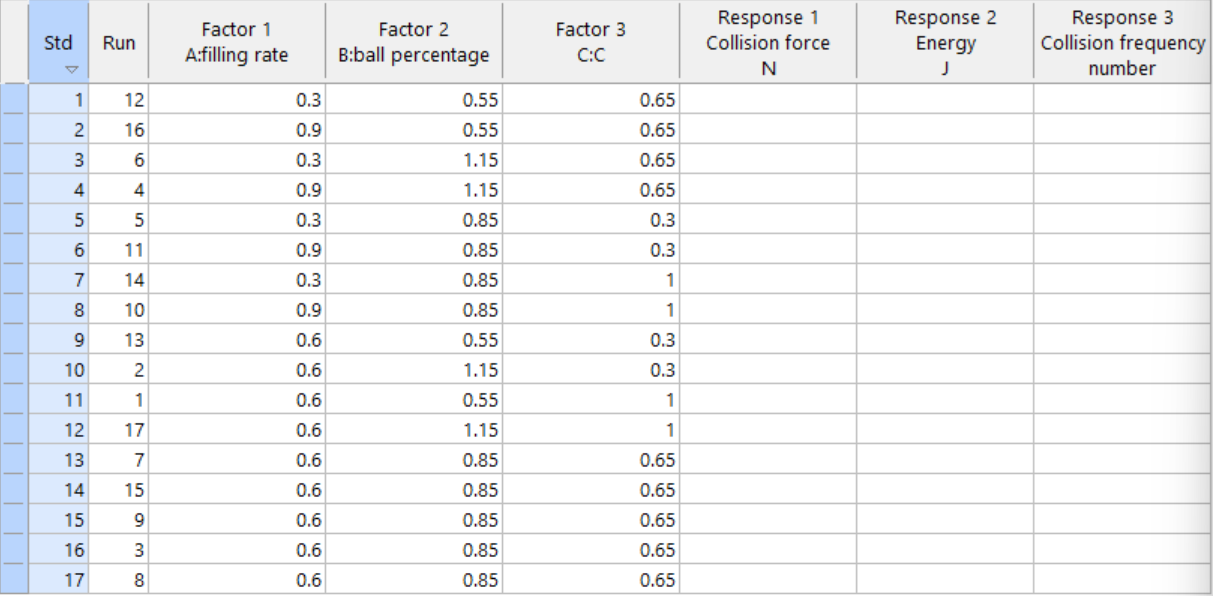
响应曲面优化实验表

通过实验获得结果后，进入左边工具栏Analysis中对应的响应值

  • 实验数据Model窗口：

若回归方程的拟合效果不佳，可以在Model窗口中修改拟合模型（线性，2FI，二次，三次等）

  • 实验数据的ANOVA分析窗口：

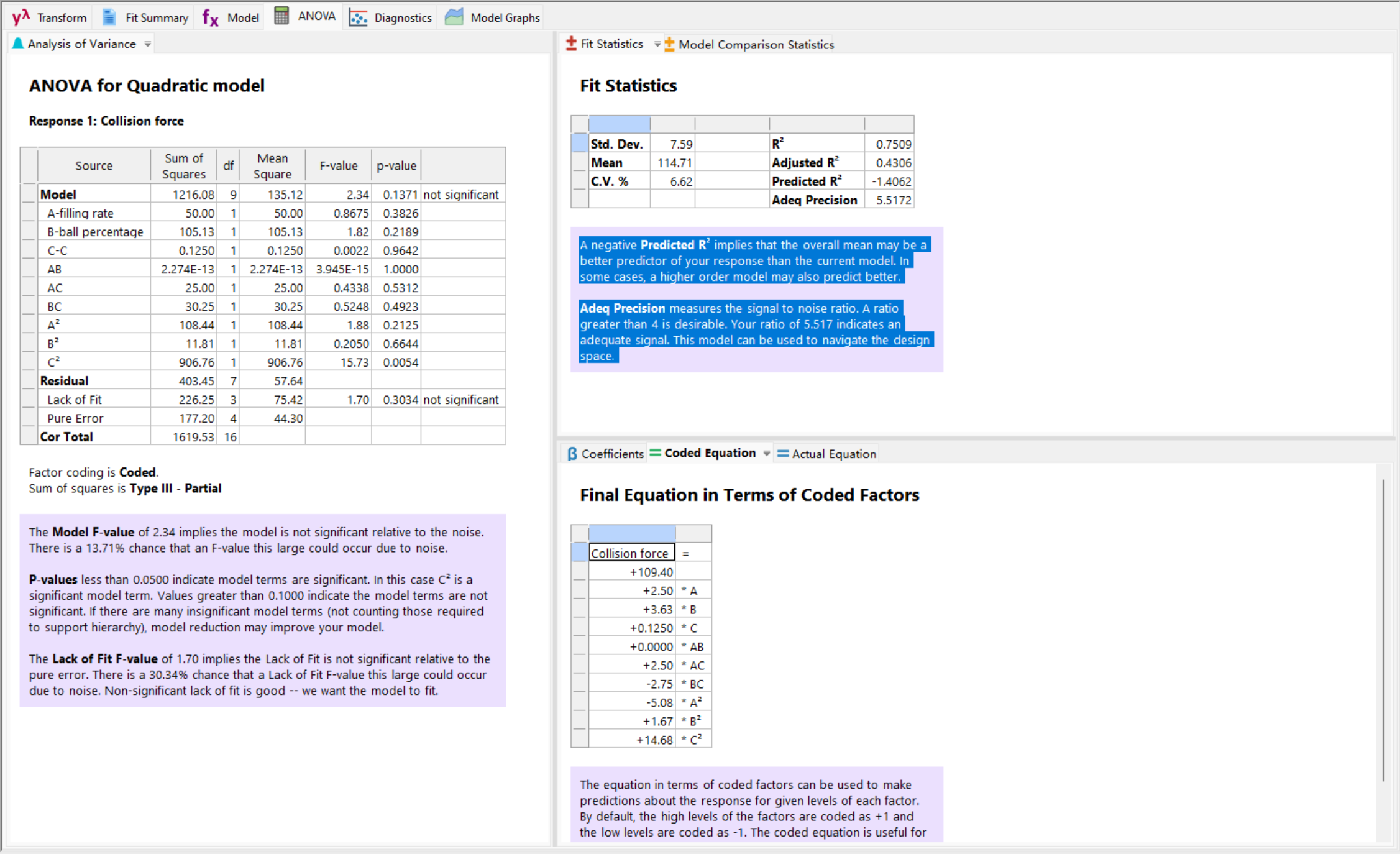
在ANOVA for Quadratic model窗口中，可以看到对于该响应值的方差分析结果。
注：一般要求第一项Model“显著”，中间的单因素实验最好表现为"显著"，最后一项Lack ofFit“不显著”

在Fit Statistics窗口的项：R2R^2和AdjR2AdjR^2的值应当接近11，AdjR2AdjR^2与PredR2PredR^2的差值应当小于0.20.2，C.V%C.V\%应当小于1010，AdegPrecisiorAdeg Precisior大于44

可以在Coded Equation中得到二次多项式回归方程

方差分析
  • 实验数据的Diagnostics 窗口：

Diagnostics Tool用于诊断模型与实验设计有效性

Normal Plot of Residuals（残差正态分布图），需要产生的数据点贴近直线
Residuals vs.Predicted（残差与预测），数据点应体现为紊乱、无规律
Predicted vs.Actual（预测与实际情况），数据点应当贴近直线

  • 实验数据的Model Graphs窗口：

在Model Graphs窗口中可以进行曲线图、折线图、等高线图、响应面图等图形的绘制。
绘图的横纵坐标标注双击后可进行修改，视角可随拖动转变，不同因素之间的影响关系可以在Contour面板中进行调整

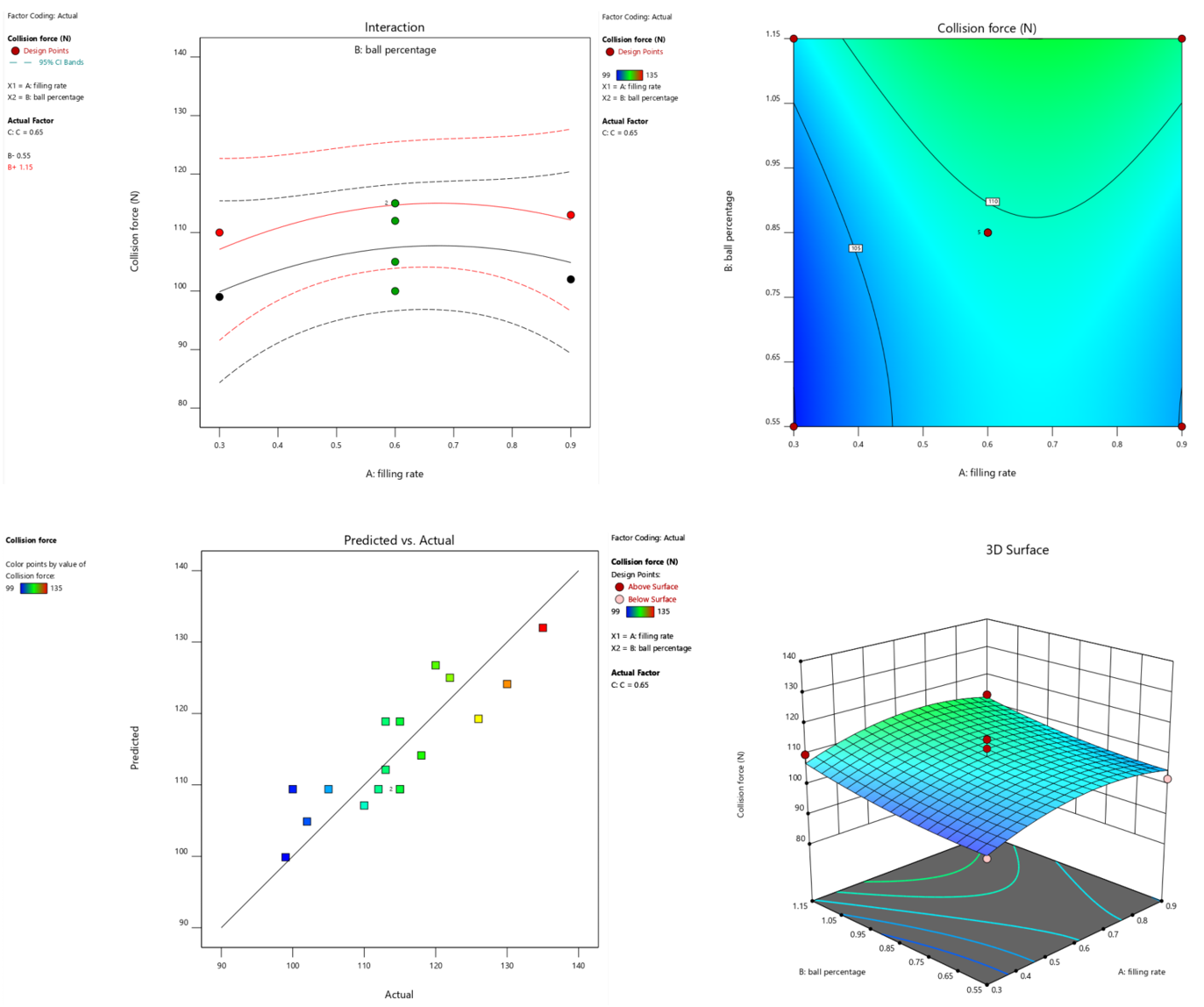
image-20230209210149308

软件中的图形也可以提取数据导入到Origin中进行绘制和调整。

注：相应操作可以参考https://www.bilibili.com/video/BV1n34y1v7kP/spm_id_from=333.999.0.0&vd_source=3d05655e912261bce2a9d4c7d27ab69d

Optimization窗口：

该窗口用于最佳工艺参数的获得，点击Optimization窗口下的Numercial
切换到Solution界面，得到该指标下各因素的最优值。

选择评价指标Solution界面

1.3文章中的应用

《基于响应面分析的附壁脉冲射流喷嘴优化设计》，三因素四水平一评价指标，CCD（中心复合设计）

响应面法 (ＲSM)是综合了数学方法和统计方法的优化设计方法，通过对局部点进行试验，从而拟合全局得到回归方程，进而得到各因素的最优水平值。通过响应面分析，可以全面分析各关键结构参数对振荡效果的影响，进而进行整体优化，同时节约计算成本。

设定了响应面试验的因素和水平与CCD设计表及模拟结果；得到了拟合的回归方程，回归方程的方差分析。通过等高线图判断因素对结果的影响大小，利用整体P值、R2R^2、CV值判断模型拟合的精确度。

检验模型适用性：模型的适应性较好时，残差的正态概率分布图中概率和残差应该在一条直线上，预测值与实际值分布图中模型的预测值和实际值应该尽量在一条直线上，残差与预测值分布图中模型的概率和预测值分布应该随机没有规律。

通过，三位立体图及等高线图中可以看出因素对评价指标的影响。响应面三维图中通过图形的凹凸程度判断因素之间交互作用知否显著。等高线图中通过等高线上的数值和区域颜色判断因素对评价指标的影响方式（正向、反向）。

《基于响应面分析的碳纤维复合材料基激光除漆工艺优化》，三因素三水平三评价指标，BBD

作为一种操作次数少、试验周期短、结果精度高的工艺参数优化方法，响应面分析法以数理统计优化为基础，通过合理且次数有限的试验设计，构建各因子与响应值的多元二次回归方程，包含各显著因子的一次项、交叉项及二次项，快速、准确地实现参数优化、响应值预测及误差分析。

设定了响应面优化试验输入因子及水平设计，给出响应面优化试验设计矩阵及试验结果。

P−valueP-value代表噪声造成误差的概率，认为 P−valueP-value小于 0.05为模型显著。

结果中罗列了三个因素的拟合模型及方差分析表，三因素对某一评价指标影响的描点图，三因素成对对某一评价指标影响的等高线图和响应面图以及最终的工艺参数优化组合。

《应用响应面分析法优化布氏菌活疫苗的冻干工艺参数》，三因素三水平一评价指标，BBD

响应面分析（RSA）法系采用多元二次回归方法作为函数估计的工具，将多因子试验中因素与指标的相互关系用多项式近拟，依此可对函数的响应面和等值线进行分析，研究因子与响应面之间、因子与因子之间的相互关系。

本文先经过单因素实验确定了理想的水平范围，再展开三因素三水平BBD实验。

将试验中一个因素固定于零水平,绘制响应曲面图和等高线图,评价另两个因素之间的交互作用,曲面越陡、等高线越密集和越接近椭圆形,则交互作用显著,而曲面越缓、等高线稀疏和越接近圆形,则交互作用不显著。

二、Minitab与混料设计

混料试验是一类特殊的响应曲面试验，其中所调查的产品由多种成分组成。设计这些试验很有用，因为工业环境下许多产品设计和开发活动都涉及配方或混料。在这些环境中，响应是混料中各种成分的比例的函数。

在最简单的混料试验中，响应（基于某些标准的产品质量或性能）取决于这些分量（成分）的相对比例。分量的量（以重量、体积或某些其他单位来度量）相加后得出标准总量。相比较而言，因子设计中的响应则随每个因子的数量而变化。

Minitab 提供三种设计（单纯形质心、单纯形格点和极端顶点）并使用以下这三类试验进行分析：

  • 混料

    假定响应仅取决于混料中各分量的比例。例如，油漆的颜色只取决于所使用的颜料。

  • 混料过程变量

    假定响应取决于各分量的相对比例和过程变量，过程变量虽是试验中不属于混料部分的因子，但它可能会影响混料的混合属性。例如，蛋糕的口味取决于烹饪时间、烹饪温度以及蛋糕成分的比例。

  • 混料总量

    假定响应取决于各分量的比例和混料的数量。例如，农作物的产量取决于杀虫剂成分的比例以及杀虫剂的施用量。

三、常见的试验优化设计方法

3.1析因设计

介绍：

析因设计是一种多因素多水平的交叉分组进行全面试验的设计方法。
它不仅可检验每个因素各水平间的差异，研究2个或2个以上因素的主效应，而且可检验各因素间的交互作用，通过比较各种组合，可以找出最佳组合。
它是一种全面的高统计效率的设计，当因素数目和水平数都不太大，且效应与因素之间的关系比较复杂时，常常采用该种设计。

数据分析：

析因设计可以提供三方面的重要信息：各因素不同水平的效应大小；各因素间的交互作用；最佳组合。

可以求出主效应和交互效应，一般分为：正交互效应(协同作用)，两因素联合(共同)作用大于其单独作用之和；负交互作用(拮抗作用)，两因素联合作用小于其单独作用之和。

优点：

可以用来分析全部主效应(即各个单因素的作用)和因素之间的各级交互作用的效应(即任何两个因素之间的交互作用效应、任何三个因素之间的交互作用效应等)的大小。

缺点：

所需要的实验次数很多(因该设计的原名也叫做“有重复实验的全因子设计”) 。当考虑的因素增加时，不但计算复杂，而且给众多交互作用的解释带来困难。

3.2正交设计

介绍：

正交试验设计是试验优化的一种常用技术。它是建立在概率论、数量统计和实践经验的基础上，运用标准化正交表安排试验方案，并对结果进行计算分析，从而快速找到最优试验方案的一种设计方法。

它是根据正交性从全面试验中挑选出部分有代表性的点进行试验，这些点并不是随便找的点，而是一些具备“均匀分散、齐整可比”的点。然后我们通过对代表性点的试验进行结果分析，进而推广到整体试验，以实现工艺的优化。

优点：

其布点均衡，试验次数减少
它能保证主要因素的各种可能都不会漏掉
它能提供一种分析结果(包括交互作用)的方法，结果直观容易分析
每个试验水平都重复相同次数，可以消除部分试验误差的干扰
因其具有正交性，易于分析出各因素的主效应。

缺点：

它提供的数据分析方法所获得的优选值，只能是试验所用水平的某种组合，优选结果不会超越所取水平的范围;
另外，也不能给进一步的试验提供明确的指向性，使试验仍然带很强的摸索性色彩，不很精确。

这样，正交试验法用在初步筛选时显得收敛速度缓慢，难于确定数据变化规律，增加试验次数。尤其在试验工作烦琐、费用昂贵的情况更显突出。

析因设计表以及正交设计表

3.3均匀设计

介绍：

均匀设计法是一种建立在正交设计上的试验设计方法。均匀设计的数学原理是数论中的一致分布理论。均匀设计只考虑试验点在试验范围内均匀散布，挑选试验代表点的出发点是“均匀分散”，而不考虑“整齐可比”。

它着重在试验范围内考虑试验点均匀散布以求通过最少的试验来获得最多的信息，因而其试验次数比正交设计明显的减少，使均匀设计特别适合于多因素多水平的试验和系统模型完全未知的情况。

均匀设计表：

每个均匀设计表有一个代号，其中 U表示均匀设计，n表示水平数亦表示试验次数，m表示该表最多可安排的因素数量。右上角加“* ”的 U表均匀性较好，应优先选用。

优点：

均匀设计使得试验次数大大减少，能够自动将各试验因素分为重要与次要，并将因素按重要性排序
时过程数字化，可通过电脑对结果与因素条件进行界定与预报(如天气预报)，进而控制各因素。

缺点：

均匀设计是非正交设计，所以它不可能估计出方差分析模型中的主效应和交互效应，但是它可以估出回归模型中因素的主效应和交互效应

3.4响应面设计

介绍：

响应面分析是一种优化工艺条件的有效、快速、精确的试验方法，系通过中心组合试验，采用多元线性回归方法为函数估计的工具，将多因素试验中的因素与水平的相互关系用多项式进行拟合，然后对函数的响应面等值线和用回归方程的分析来寻求最优工艺参数，可精确地描述因素与响应值之间的关系。

响应面法(RSM)主要有三种常用的试验设计方案：Box-Behnken设计(BBD)、均匀外壳设计(UniformShellDesign，USD)和中心组合设计(CentralCompositeDesign，CCD)。前两种较少使用，中心组合设计是响应曲面中最常用的二阶设计。CCD设计是多因素5水平的实验设计，是在二水平析因设计的基础上加上极值点和中心点构成的

优点：

相比于正交设计和均匀设计，响应面设计法得到的回归方程精度高，能够得到几种因素间交互作用等优点
RSM能够将优化过程延伸到面的程度，呈现三维立体效果。
同时RSM能够减少最佳条件下效应的预测值和实测值偏差，具有突出的优越性。

缺点：

相对于因子分析，精度仍不够，它要求自变量必须是连续的而且能被试验者自由控制，如果先用 CCD找到最优区，再使用因子分析在较小的范围内应用效应面优化法则效果会更好。

中心复合设计 (Central composite designs,CCDs)：

也称为Box-Wilson设计，适用于建立完整的二次模型（带交互项）。有三种类型的CCD，每个设计都包含一个中心点和多个卫星点，以允许估计二阶效果。这样，对于一个含n个因素的二次模型，CCD就有足够多的点来估计二次模型所有的系数（二次模型一共有（n+2）（n+1）/2个系数）。CCD又分三种：

（1）外接式(circumscribed，CCC)

（2）内接式(inscribed，CCI)

（3）外侧面式(faced，CCF)

中心复合设计

Box-Behnken设计：

与CCD中描述的设计一样，Box-Behnken设计用于建立完整的二次模型。Box-Behnken的设计是可旋转的，并且对于少数因素(4个或更少)，比CCD需要更少的样本。通过避免设计空间的角落，他们允许实验者绕过极端的水平组合。当然，对极端情况的估计也差了一点。Box-Behnken设计的几何图形继续看图说话：

Box-Behnken设计

3.5拉丁超立方取样